ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Chandana. Raj1, Dr. Keshaveni. N2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This project is focused on developing hardware implementations of image processing algorithm for use in an FPGA -based image processing system, this approach facilitates comparison of the software and synthesized hardware algorithm outputs. The rank order filter is a particularly common algorithm in image processing systems. This approach was taken because it speeds understanding of the algorithm design, reduces the number of comparison, and the area required. For every pixel in an image, the window of neighbouring pixels is found. Then the pixel values are sorted in ascending, or rank, order. Next, the pixel in the output image corresponding to the origin pixel in the input image is replaced with the value specified by the filter order. The main advantage of the sorting network is that the sequence of comparisons is fixed. Thus it is suitable for parallel processing and hardware implementation, especially if the number of sorted elements is small. The number of compare–swap components and delay are two crucial parameters of any sorting network. By delay we mean the minimal number of groups of compare–swap components that must be executed sequentially. This algorithm ensures the number of comparators and delay used for given input and reduces the number of comparisons and computation time.
Keywords |
| spatial filtering, window, 2D mask, kernel, impulsive noise. |
INTRODUCTION |
| Although seemingly easy for living beings, coping with vision is less natural for computers. Images need to be captured, digitized and processed until some form of decision or conclusion can be made. Thus image processing, the analysis and manipulation of data, originally in the form of an image or image sequence, by a computer is acknowledged as one of the grand challenges of computing. The reasons for this are: Data size, Computation complexity, Time constraints, Types of operations, Variety in image processing algorithms, Different data types. Image processing tasks such as filtering, stereo correspondence and feature detection are inherently highly parallelisable. The use of FPGAs (Field Programmable Gate Arrays), which can be operated in highly parallel configurations, can thus be a useful approach in imaging applications. The median filter is a non-linear filter; it is a special case of rank order filters whose rank is half the length of the sequence. In image processing applications, median filter is used to remove impulsive noise from images while preserving the edges. One of the disadvantages of linear filters, such as the moving average filter, when used to denoise the data, is that they not only smooth the noise, but also smooth the sudden and sharp transitions that were present in the original data, such as edges in images. Moreover, they are not as efficient as the median filters in removing certain types of noise, such as impulsive noise Although median filters do not blur the edges as much as the linear filters do, because they still possess smoothing characteristics, as the size of the filter increases, there may be significant image blurring. In image processing, the 2D filtering operation is performed by sliding the window along all the rows and columns of the image until all the pixels are covered by the window. Median filtering techniques are usually based on the sorting network architectures; another approach to implement the median filter is based on the histogram. The resources required to implement the sorting network architecture on a FPGA device increases with the size of the filtering window. However, the sorting network based algorithms are independent of the size of the image and depend only on the size of the window. |
DESCRIPTION OF MEDIAN FILTER |
| Median filter is often applied to gray value images due to its property of edge preserving smoothing. The main idea of the median filter is to run through the signal entry by entry, replacing each entry with the median of neighbouring entries. The pattern of neighbours is called the "window", which slides, entry by entry, over the entire signal. For 1D signals:, the most obvious window is just the first few preceding and following entries, for 2D (or higher-dimensional) signals such as images, more complex window patterns are possible (such as "box" or "cross" patterns). If the window has an odd number of entries, then the median is simple to define: it is just the middle value after all the entries in the window are sorted numerically [2]. For an even number of entries, there is more than one possible median, see median for more details. Like the mean filter, the median filter considers each pixel in the image in turn and looks at its nearby neighbours to decide whether or not it is representative of its surroundings. Instead of simply replacing the pixel value with the mean of neighbouring pixel values, it replaces it with the median of those values [1]. The median is a more robust average than the mean and so a single very unrepresentative pixel in a neighbourhood will not affect the median value significantly. Since the median value must actually be the value of one of the pixels in the neighbourhood, the median filter does not create new unrealistic pixel values when the filter straddles an edge. For this reason the median filter is much better at preserving sharp edges than the mean filter. In general, the median filter allows a great deal of high spatial frequency detail to pass while remaining very effective at removing noise on images where less than half of the pixels in a smoothing neighbourhood have been effected. To find the median it is necessary to sort all the values in the neighbourhood into numerical order and this is relatively slow, even with fast sorting algorithms such as quick sort. The basic algorithm can, however, be enhanced somewhat for speed. A common technique is to notice that when the neighbourhood window is slid across the image, many of the pixels in the window are the same from one step to the next, and the relative ordering of these with each other will obviously not have changed. To apply the mask means to centre it in a pixel, evaluating the covered pixel brightness’s and determining which brightness value is the median value [4]. The median value is determined by placing the brightness’s in ascending order and selecting the centre value. |
ARCHITECTURE |
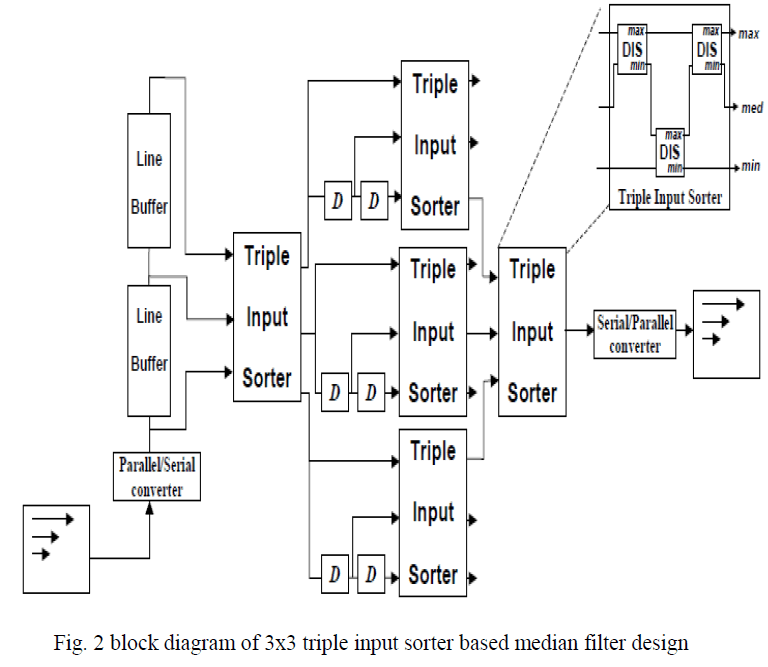
| Requiring on the median value, then there is no need for sorting the .whole window. An optimized version of the Bubble sorter is presented in Figure 1, for the special case of a 3x3 window. The architecture is based on a Triple Input Sorter [6] and consists of the following stages Stage 1: Sorts the elements of each window column. Stage 2: Sorts the elements of each window row. Stage 3: The median is finally obtained by sorting the cross diagonal and picking up the middle value. Only three results are guaranteed to be placed in the right place: the maximum, the minimum and the median; this saves a great deal of logic. The main component in this design is a Triple Input Sorter (which is based on a dual input sorter), Triple Input Sorter based algorithm (TIS) which is an optimized version of the Bubble sort algorithm for the special case of a 3x3 window size which is as shown in fig2. During the median filter step 9 neighbouring pixels including the centre pixel are assigned to three row extractors for shortening the searching time of the median value. At first, each row extractor extracts the median value of three pixels in its row. The three row extractors work in parallel, which is one operation level parallel. Then, the final median extractor calculates the median value of the output values of three row extractors. This improvement will greatly expedite the process of median searching [5]. |
 |
 |
| Equations: |
| In simple terms , scanning through the image pixels by a 3 * 3 matrix calculate the median by sorting the values then we replace the pixel being considered with the middle pixel value (if we have even number of pixels then we use average of the two middle pixel), as shown in fig1 |
| The classic median filter is also a subset of a more general set of filters, called rank order filters, which are themselves a subset of stack filters [7]. As in median filtering, a 2-D rank order filter consists in passing a PxQ window over an image and computing a result pixel from the sample pixel values S = (S1, S2, ……, SP*Q) within the window. The basic 2D (3 * 3) median filter is characterized by the following equation: |
 |
SYSTEM IMPLEMENTATION |
| A. System overview: Prior to any hardware design, the software versions of the algorithms are created in MATLAB. Using MATLAB procedural routines to operate on images represented as matrix data, these software algorithms were designed to resemble the hardware algorithms as closely as possible. This approach was taken because it speeds understanding of the algorithm design. In addition, this approach facilitates comparison of the software and synthesized hardware algorithm outputs. When the median filter must be carried out in real time, the software implementation in general purpose processors does not usually give good results. |
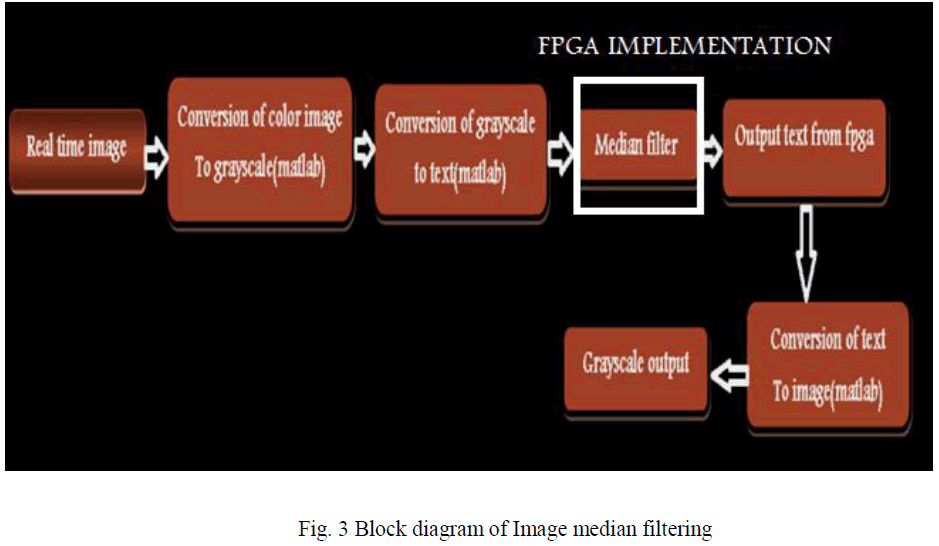 |
| Reconfigurable computing architectures [1], [2] are sufficiently flexible so that new operations can be implemented in the existent hardware, and they are quite quick for real-time execution. Conversion of a colour image to gray scale is not unique; different weighting of the colour channels effectively represent the effect of shooting black-and-white film with different-colored photographic filters. Real time images from web cam are taken and processed in matlab which first converts the real time color image to gray scale, which is in turn converted to text file which is given as a input to median filter on FPGA through Xilinx which process in finding the median value of image by removing the salt and pepper noise present in image without any blurring of image by edge preservation and is back converted using matlab. |
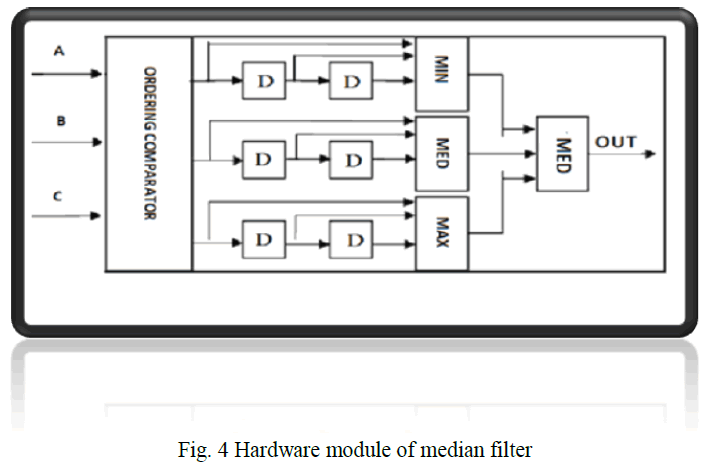
| B. Hardware implementation of median filter module: A sorting algorithm is an algorithm that puts elements of a list in a certain order. Efficient sorting is important for optimizing the use of other algorithms (such as search and merge algorithms) which require input data to be in sorted lists. Bubble sort is a simple sorting algorithm. Median filtering techniques are usually based on the sorting network architectures, These sorting networks use compare and delay units to implement the median filter. The incoming pixels are passed through a network of comparators and swapping units - the comparator units compare two to three incoming pixels at once and then the swapping unit sorts them accordingly. The algorithm starts at the beginning of the data set. It compares the first two elements, and if the first is greater than the second, it swaps them. It continues doing this for each pair of adjacent elements to the end of the data set. It then starts again with the first two elements, repeating until no swaps have occurred on the last pass. Because we can get the maxim value or the minimum value of 3 data by doing 2 comparisons, and get the median value or the ordering of 3 data by doing 3 comparisons, we design 4 different comparators, such as ordering comparator, minimum comparator, median comparator and maxim comparator [5]. The hardware structures of the 4 comparators are given in figure 3. the processing element is basic processing unit, which is designed for comparing 2 input data. D stands for D flip-flop, whose function is to make a single-circle delay. It is used for synchronizing the calculation here. Because the proposed algorithm needs to storage two groups temporary data in current processing, we design two D flip-flops to realize this function [1]. The data’s will be sent to the ordering comparator ordinally for data ordering, and the results will be send to next different comparators. Before the second comparing, the data need 2 circle delay to distinguish the circle order of input data by two D flipflops. The second comparing results will be sent to the final median comparator to get the final result. |
 |
| The median value will be the middle value of the sorting network. It utilize 3×3 masks, which means that processing each pixel, as the pixels in the boundary of each section, needs eight pixels around it. In order to deal with the boundary problem, each section contains four more rows of pixels than half input image. The four extra rows are responsible for processing a boundary row. |
RESULT |
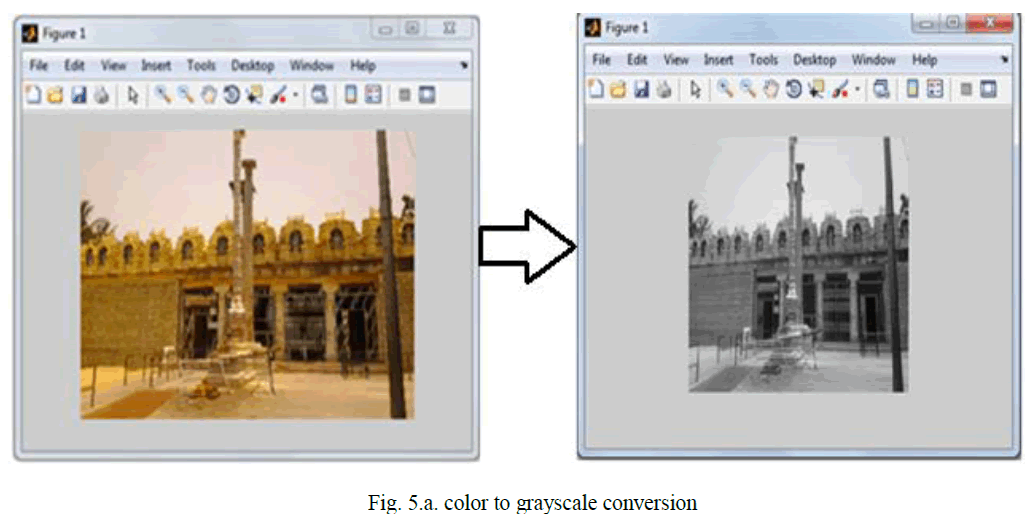
| This algorithm is applied for 3x3 median filter on a real time image. since median filter Is very effective in removing the salt and pepper noise more effectively in gray scale the real time color image is converted to gray scale and the processing is carried out as shown in fig. 5.a |
 |
 |
| The fig.5.b shows the text format of the gray scale image done in Matlab, which is then given as input to FPGA for median filtering. |
 |
| Fig.5.c shows the simulation results of the median value calculation with very less computation from the first output to the last output, which has the great impact on the speed of image processing on real time application. |
| The computation time from reset output to the first output available is comparatively smaller than the traditional median filtering algorithm. |
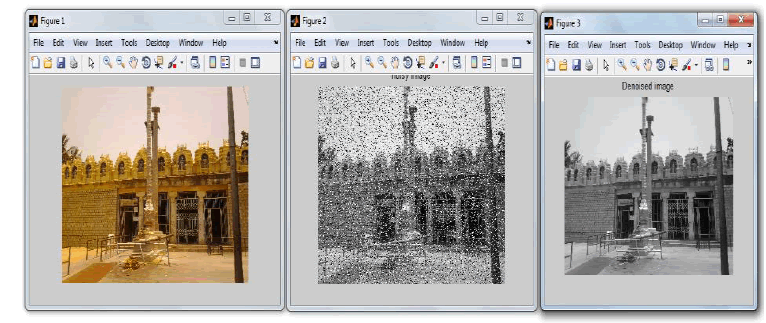 |
| Fig. 5.d. Matlab Results of median filter with filtered and denoised output image in grayscale Fig 5.d shows the Matlab output with real time color image getting converted to grayscale and median filtering on FPGA is performed, as it is very effective in removing the impulsive noise like salt and pepper noise without any blurring of original image. |
CONCLUSION |
| The experimented results show that it can effectively reduce the issues of real time applications, with less computation time by reducing the number of unnecessary comparisons, pixel memory and the size of the memory which are made independent of any image sizes. The image median filtering is done in both on FPGA and Matlab which provides a door to comparison of hardware and software results. Despite the effectiveness of spatial domain technique s when applied separately, in practice a combination of such methods can be used to achieve more effective image enhancement. This effectively removes the impulsive noise and preserving the edges with smaller computation time and lesser area required. This approach is highly parallelizable. Nonlinear filters offers a flexible, robust approach to the problem of estimating signals in the presence of impulsive noise. |
ACKNOWLEDGMENT |
| This paper is made possible through the help and support from parents, teachers, friends I sincerely wish to thank them all. |
References |
|