ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
K.Lakshmi Sowjanya, Dr L.Ravi Srinivas,
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
PID controllers are most popular controllers because of simplicity of implementation and broad applicability. In order to obtain the desired control performance correct tuning of PID controller is very important. There are many tuning algorithms available for tuning the PID controller. Most of the tuning processes are implemented manually. These processes are difficult and time consuming. Soft computing techniques have been widely used to tune the parameters of PID. In this paper parameters of PID controller are tuned using two sets of soft computing techniques which are Differential Evolution (DE) and Hybrid Differential Evolution (HDE). The optimal PID control parameters are applied for a composition control system. The performance of two techniques is evaluated by setting its objective function with Integral Square Error (ISE), Integral Absolute Error (IAE), Integral of Time multiplied by Absolute Error (ITAE). This paper also compares performance of tuned PID controller using DE and HDE methods with Ziegler-Nichols method.
Keywords |
| Differential Evolution, Hybrid Differential Evolution and PID Controller. |
INTRODUCTION |
| PID controllers are most widely used in industries such as oil and gas, chemical etc.PID controlled has been proven in terms of reliability and robustness in controlling the process variables. Other factors that attracted industries to choose PID could be due to low cost, easy to maintain as well as simplicity in control structure and easy to understand. The PID controller calculation involves three separate parameters: proportional, integral and derivative values. The proportional value calculates the value of the current error, the integral value determines the result of sum of recent errors and derivative value determines the reaction based on the rate at which the error has been changing. The weighted sum of these three actions is used to be imported into the controlled system. However in practice, the controlled system systems usually have some features, such as nonlinearity, time-variability and time delay, which make controller parameters tuning more complex. Thus the goal of PID controller tuning is to determine parameter parameters that meet the closed-loop system performance specifications over a wide range of operating conditions. Improper PID parameters tuning could lead to cyclic and slow recovery, poor robustness would be the collapse of system operation [1].This lead researches to explore the best tuning method in searching optimum PID parameters. Many strategies have been proposed to determine optimum setting of PID parameters. Ziegler-Nichols and cohen-coon are the most popular PID tuning methods. Among the conventional PID tuning methods Ziegler-Nichols (ZN) method may be the well known technique. However sometimes it does not provide good tuning and tends to produce big overshoot. To enhance the capabilities of traditional PID parameters tuning techniques, several soft computing techniques have been suggested, such as those based on Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Differential Evolution (DE), Ant Colony Optimization (ACO).DE was introduced by Rainer Storn and Kenneth Price. Many practical problems have objective functions that are non differentiable, nonlinear noisy. DE can be used to find approximate solutions to such problems. This paper presents development of an optimal PID controller for a higher order system and composition control system using DE and HDE techniques. This paper also compares the transient performance of the two systems using DE and HDE tuning methods with Ziegler-Nichols method. |
COMPOSITE CONTROL SYSTEM |
| Composite control system was designed to control liquid level in a three tank system. Composite Control system consists control reagent tank, tank1, tank2, tank3.Control Reagent tank contains water and solution. |
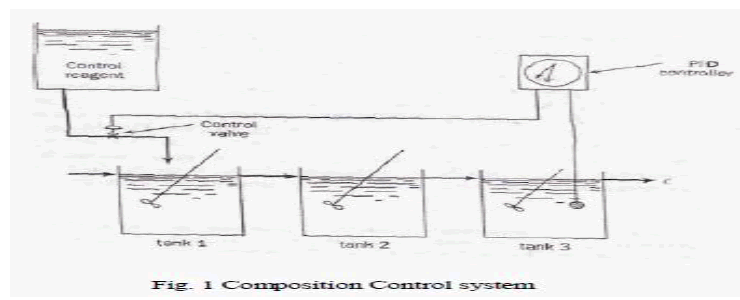 |
| It control the liquid level in tank1, tank2, tank3.Control of liquid level was accomplished by control valve which is operated by PID controller. Liquid flows from control reagent tank to tank1, then tank1 to tank2 and finally tank2 to tank3.The level of liquid in third tank is sent to the controller. The controller generates a signal which opens or closes the control valve. Based on control valve operation liquid level in three tank system is controlled. The time constant and steady state gain of control reagent tank is chosen as 5 and one. The time constant and steady state gain of three tanks is chosen as one. The block diagram representation of the system is shown in fig.2. |
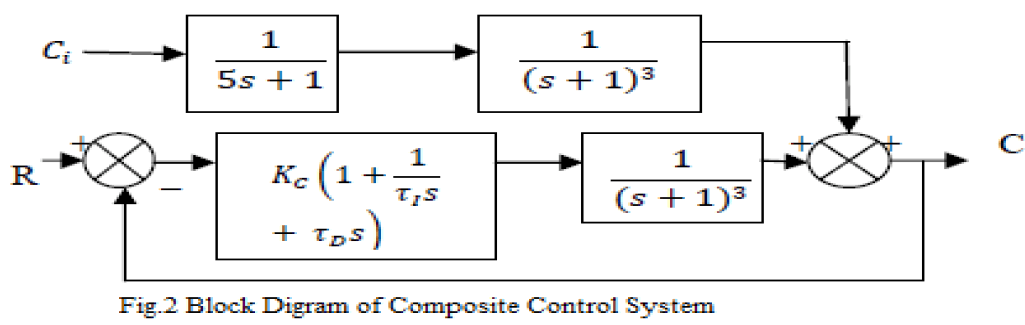 |
| Where R is the set-point, C is the output of three tanks that is height of liquid level and Ci is the input from the control reagent tank. The transfer function of the system shown in fig.2 is |
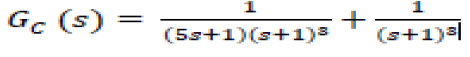 |
| Many methods are available for tuning the PID controller. The most widely used method is Ziegler-Nichols method. Though Ziegler-Nichols method is simple and most popular it has some disadvantages. It gives large overshoot and prior knowledge regarding plant model. If the plant is tuned by the Ziegler-Nichols method it gives good results but those are not optimum. To enhance the PID parameter tuning techniques soft computing techniques have been suggested. Some of the techniques are Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Differential Evolution (DE), and Ant Colony Optimization (ACO). |
PID CONTROLLER |
| PID controller consists of three separate PID controller consists of three separate parameters: proportional, integral and derivative with gains denoted by Kp, Ki, Kd. Appropriate setting of these parameters will improve dynamic response of a system, reduce over shoot eliminate steady state error and increase stability of the system. The transfer function of a PID controller is |
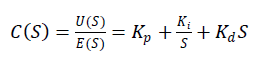 |
| Once the input has been changed, the error will be computed between the input and actual output. The error signal, E(s), is used to generate the proportional, integral, and derivative actions. With the resulting signals weighted and summed to form the control signal U(s), applied to the plant model. The new output signal will be obtained. This new actual output signal will be sent to the controller, and again error signal will be computed. New control signal, U(s) will be sent to the plant. This process will run continuously until the steady state error. |
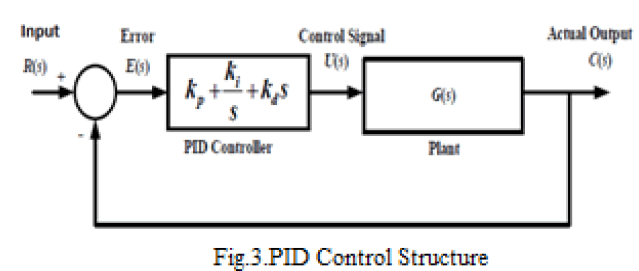 |
DIFFERENTIAL EVOLUTION |
| Evolutionary Algorithms are part of derivative free optimization and search methods. Evolutionary algorithm is an umbrella term used to describe computer based problem solving systems which use computational models of evolutionary processes as key elements in their design and implementation. Some of the examples of evolutionary algorithms are Genetic Algorithm (GA), Differential Evolution (DE) and so on. They all share a common conceptual base of simulating the Evolution of individual structures via processes of selection, mutation and crossover. The processes depend on the perceived performance of the individual structures as defined by an environment. Differential Evolution algorithm is a new heustric approach.DE algorithm is a population based algorithm like genetic algorithms using similar operators’ crossover, mutation and selection. Although many genetic algorithm versions have been developed, they are still time consuming. In order to overcome this disadvantage the evolution strategy called DE has been recently proposed by Storn and Price in 1997.Differential Evolution (DE) which has proved to be an effective algorithm amongst the best known direct search approaches for nonlinear, non-differentiable objective functions. It has been applied to several engineering and optimization problems in different areas. The main difference between genetic algorithm and DE is mutation scheme that makes DE self adaptive. Genetic algorithms rely on crossover while DE relies on mutation operation. This main operation is based on the differences of randomly sampled pairs of solutions in the population. The algorithm uses mutation operation as a search mechanism and selection operation to direct the search toward the prospective regions in the search space. In DE all solutions have the same chance of being selected as parents without dependence of their fitness value.DE employs a greedy selection process. The DE algorithm also uses non-uniform crossover that can take child vector parameters from one parent more often than it does from others. By using the components of the existing population members to construct trial vectors, recombination (crossover) operator efficiently shuffles information about successful combinations, enabling the search for a better solution space. This population is successfully improved by applying mutation, crossover and selection operators. It creates new candidates solutions by combining the individual and several other individuals of the same population. DE generates new vectors of parameter by adding the weighted difference between two population vectors to a third one. A candidate replaces the parent only if it has better fitness value. The main steps of the DE algorithm are initialization, evaluation, repeat, mutation, recombination, evaluation, selection. Algorithm of DE is |
| Step-1:Set up the control parameters of DE optimization process that are population size, scaling factor, crossover probability, convergence criterion, number of problem variables, lower and limits of variables and maximum number of iterations. Create an initial population of individuals with random positions. |
| Step-2: For each particle calculate the value of fitness function. |
| Step-3: Compare the fitness of each particle with personal best (Pbest).If current solution is better than Pbest then replace Pbest by current solution. |
| Step-4: Compare the fitness of all particles with global best (Gbest).If the fitness of any particle is better than Gbest, then replace Gbest. |
| Step-5(Mutation): DE generates a new parameter by adding the weighted difference between two vectors to a third vector. Mutant vector is generated based on the present individuals |
| Where F is called scaling factor or mutant factor which amplifies the differential variation of eq-10.Mutant vector should not be less than a certain value to prevent premature convergence. The range of mutation factor is between zero and one.r1, r2, r3, r4 are mutually distinct points taken randomly from population not coinciding with the current control parameter. |
| Step-6(Crossover Operation): The mutant vectors are mixed with the vector called target vector to form a new vector called trial vector. The parameter mixing is called crossover. Each generation of ith individual is reproduced from mutant vector +1and present individual . |
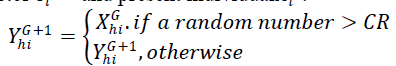 |
| Where CR is called crossover probability which affects the number the number of variables to be changed in the trial vectors compare to the target vectors.Crossover operation helps to increase the diversity among the mutant parameter vectors. Crossover constant is usually selected from within the range [0, 1]. |
| Step-7(Selection): All the solutions in the population have the same chance of being selected as parents without dependence of their fitness value. The offspring produced after the mutation and crossover operations is evaluated. Then the performance of the offspring vector and its parent is compared and better one is selected. The parent is replaced by its offspring if the fitness of the offspring is better than that of parent. |
| Step-8: Repeat steps 2 to 7 until desired fitness is reached. |
EVALUATION OF FITNESS FUNCTION |
| The fitness function considered here is based on error criterion. This work utilizes performance indices as objective function. Controller performance is evaluated in terms of integral square error (ISE), integral absolute error (IAE), integral time multiplied by absolute error (ITAE).PID controller is tuned based on the minimum value of performance index. |
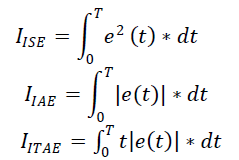 |
HYBRID DIFFERENTIAL EVOLUTION |
| The aim of optimization is to determine best suited solution to a problem under a given circumstances. Mathematically an optimization problem involves a fitness function describing the problem under a set of constraints representing the solution space for the problem. Unfortunately, most of traditional optimization techniques are centered around evaluating the first derivatives to locate the optima on a given constrained surface. Because of the difficulties in evaluating the first derivatives, to locate the optima for many rough and discontinuous optimization surfaces several derivative free optimization algorithms have emerged. One of the algorithms is Differential Evolution.DE can be used to solve complex non linear non continuous, noisy multidimensional optimization problems. In mid 1990s Storn and Price took a serious attempt to replace the classical crossover and mutation operators in GA by alternative operators and consequently came up with a suitable differential operator to handle the problem. In 1995 Storn and Price proposed a new floating point encoded evolutionary algorithm for global optimization and named it DE owing to a special kind of differential operator.DE algorithm is a population based algorithm like genetic algorithms using similar operator’s crossover, mutation and selection. Although many genetic algorithm versions have been developed, they are still time consuming. In order to overcome this disadvantage the evolution strategy called DE has been proposed. Advantages of DE are simple structure, ease of use, speed and robustness.DE has disadvantages. Parameters of DE are problem dependent and choice of them is often critical for the performance of DE. Choosing the best among the different mutation schemes available for DE is also not easy for specific problems such as in shaping optimization problems. Although DE is good at exploring the search space and locating the region of global minimum it is slow at the exploiting the search space. In order to balance the exploration and the exploitation of DE a hybrid DE with BBO is referred for global optimization problems. In DE\BBO a hybrid migration operator is proposed which combines the exploration of the original DE algorithm with the exploitation of BBO. BBO is a Biogeography-Based Optimization (BBO), proposed by Simon is a new global optimization algorithm based on the biogeography theory which is the study of the geographical distribution of biological organisms. Similar to GAs, BBO is a population based stochastic global optimizer. In the original BBO algorithm, each solution of the population is a vector of integers.BBO adopts the migration operator to share information between solutions. The main operator in HDE is migration operator which hybridizes the DE operator with migration operator of BBO. The idea of proposing the migration operator is based on two considerations. First, good solutions would be less destroyed, while poor solutions can accept a lot of new features from good solutions. In this sense, the current population can be exploited sufficiently. Second, the mutation operator of DE is able to explore the new search space and make the algorithm more robust. The algorithm of HDE is as follows Step-1:Set up the control parameters of HDE optimization process that are population size, scaling factor, crossover probability, convergence criterion, number of problem variables, lower and limits of variables and maximum number of iterations. Create an initial population of individuals with random positions. |
| Step-2: For each particle calculate the value of fitness function. |
| Step-3: Compare the fitness of each particle with personal best (Pbest).If current solution is better than Pbest then replace Pbest by current solution. |
| Step-4: Compare the fitness of all particles with global best (Gbest).If the fitness of any particle is better than Gbest, and then replace Gbest. |
| Step-5(Mutation): HDE generates a new parameter by adding the weighted difference between two vectors to a third vector. Mutant vector is generated based on the present individuals |
| Where F is called scaling factor or mutant factor which amplifies the differential variation of eq-10.Mutant vector should not be less than a certain value to prevent premature convergence. The range of mutation factor is between zero and one.r1, r2, r3, r4 are mutually distinct points taken randomly from population not coinciding with the current control parameter. |
| Step-6(Crossover Operation): The mutant vectors are mixed with the vector called target vector to form a new vector called trial vector. The parameter mixing is called crossover. Each generation of ith individual is reproduced from mutant vector +1and present individual . |
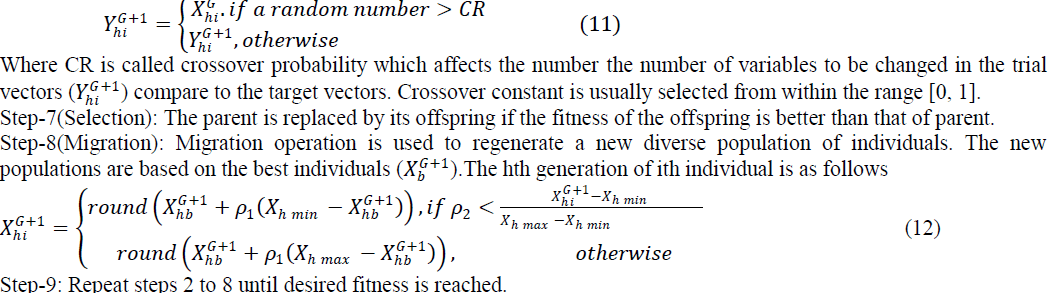 |
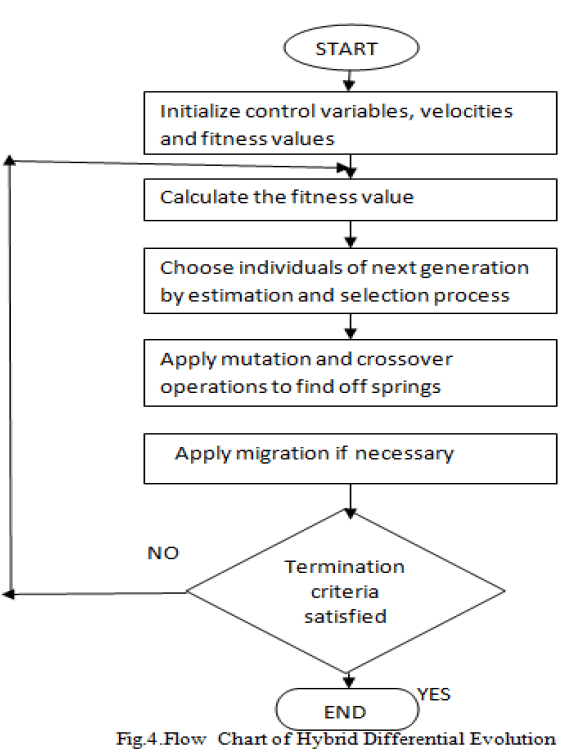 |
IMPLIMENTATION PID CONTROLLER TUNING |
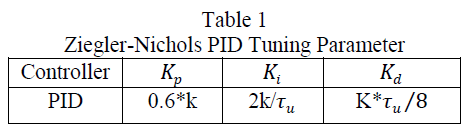
| In this section the performance of composite control system with Ziegler-Nichols method, DE and HDE is evaluated. The tuning performance is evaluated using integral square error(ISE),integral absolute error(IAE),integral of time multiplied by absolute error (ITAE).PSO and HDE find optimum value of control parameters where the smaller the value of fitness function. The transient performance of the system tuned by PSO and HDE is compared with Ziegler- Nichols method.Tuning of PID controller using Ziegler-Nichols is based on frequency response of closed-loop system by determining the point of marginal stability under pure proportional control. The proportional gain is increased until the system becomes marginal stable. At this point, the value of proportional gain is known as ultimate gain k together with its period of oscillation frequency so called ultimate period . Based on these values tuning parameters are calculated as shown in table 1 |
 |
| For mathematical model system the ultimate gain and ultimate period can be calculated using Routh-Hurwitz criterion. The PID tuning parameters are calculated and those are = 3.7, = 1.8 = 1.8. |
SIMULATION RESULTS |
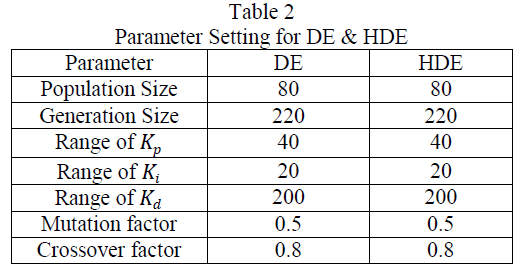
| In this section PSO is applied to find the optimal parameters of PID controller for the closed loop controlled composite control system. The parameter values of PSO and HDE optimization are shown in table 2 .The performance of tuning method is observed in terms of rise time, overshoot, peak time, settling time and steady state error. |
 |
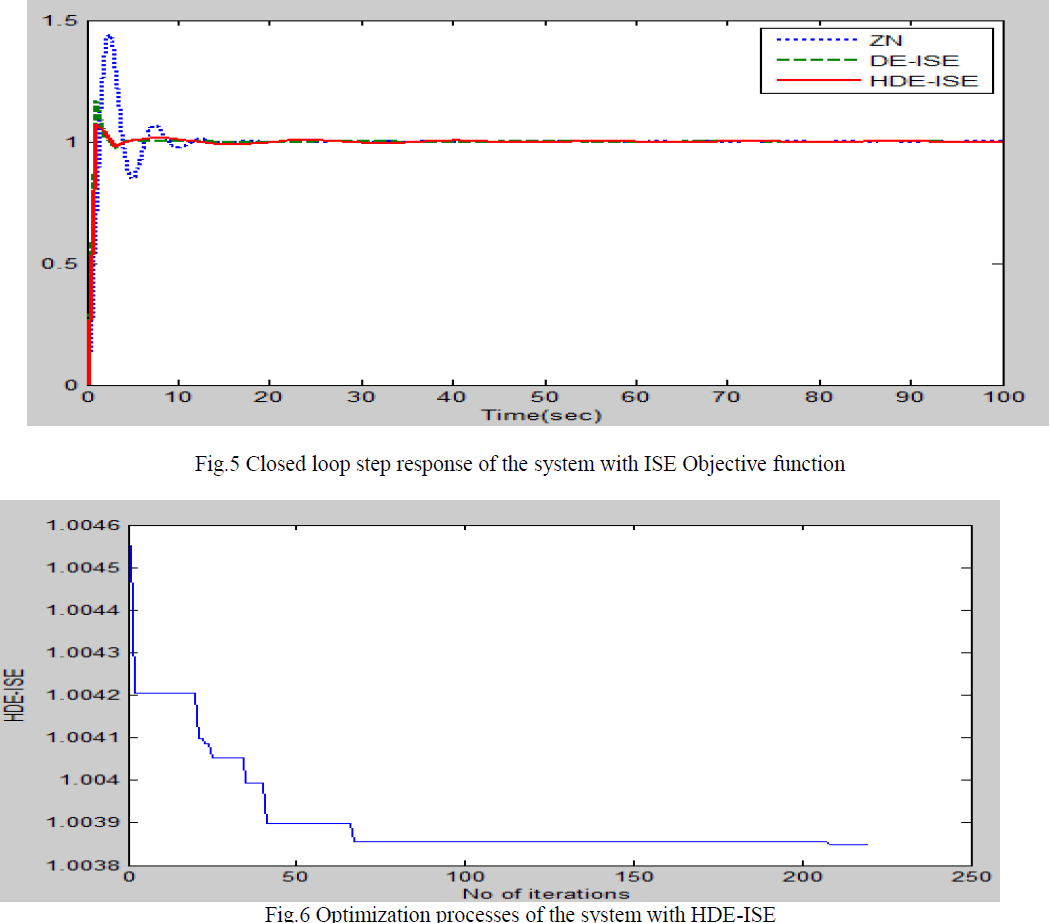 |
| PID controller was tuned based on the respective parameters for 220 iterations. Global best solution was selected for which had the minimum ISE. It was seen that ISE value tends to decrease for a large of iterations. |
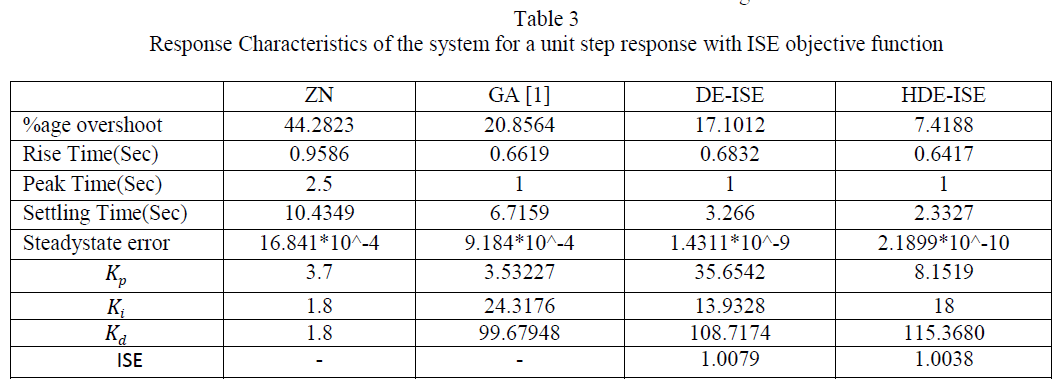 |
| PID controller has been tuned using ZN method,DE&HDE technique.For the same population, crossover rate and number of generations HDE technique gives better performance than DE,ZN and GA. |
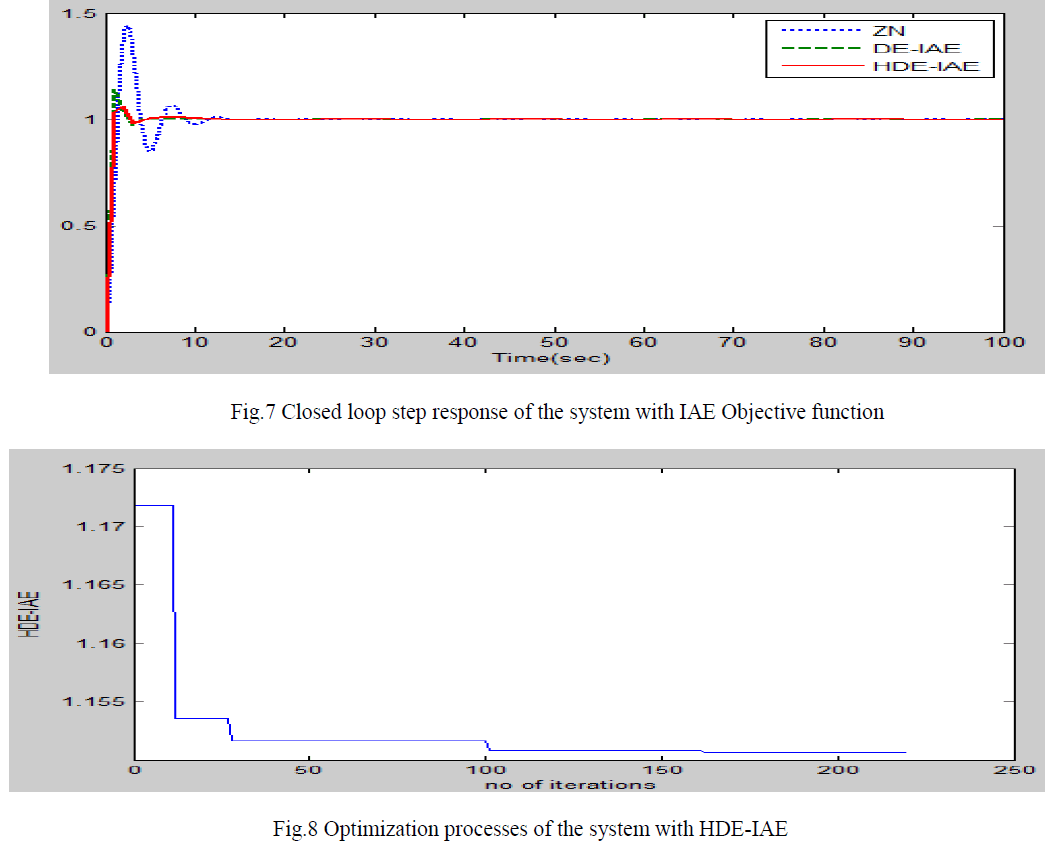 |
| PID controller was tuned based on the respective parameters for 220 iterations. Global best solution was selected for which had the minimum IAE. It was seen that IAE value tends to decrease for a large of iterations. |
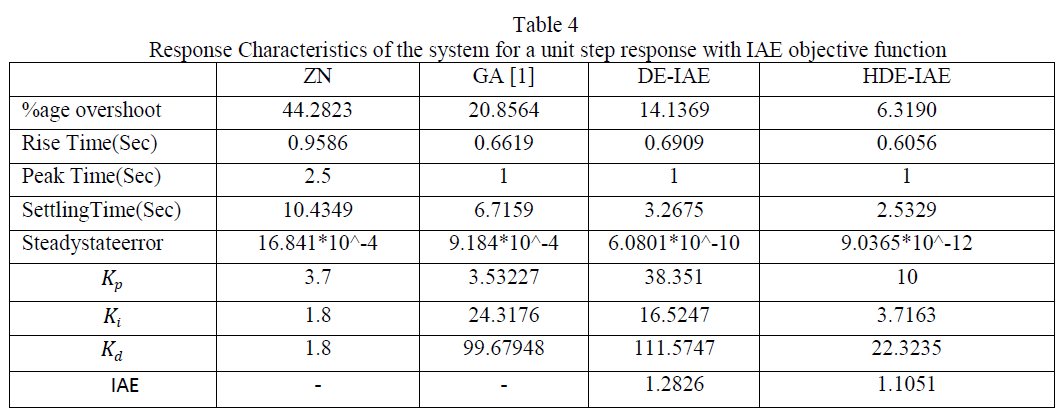 |
| PID controller has been tuned using ZN method,DE&HDE technique.However DE&HDE is optimized by IAEgives better performance than ZN .Between DE & HDE HDE gives better transient response than other techniques. |
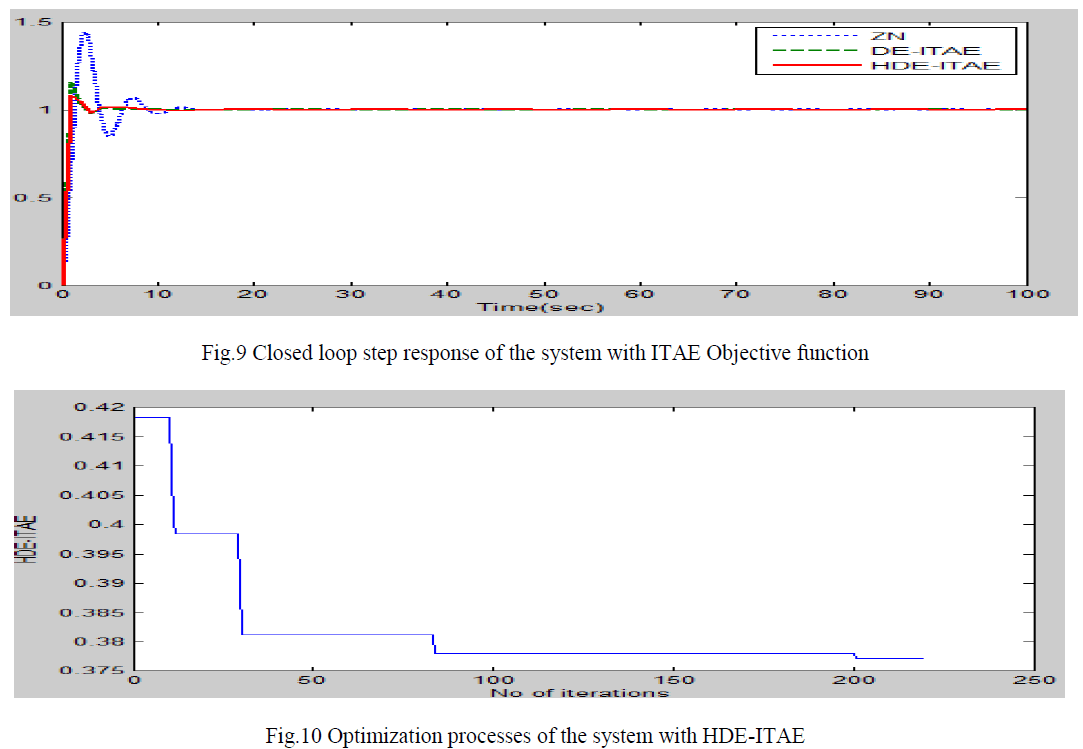 |
| PID controller was tuned based on the respective parameters for 220 iterations. Global best solution was selected for which had the minimum ITAE. It was seen that ITAE value tends to decrease for a large of iterations. |
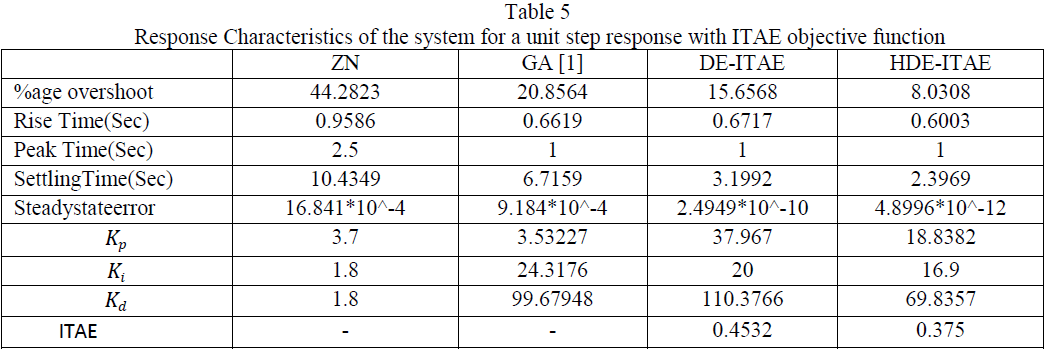 |
| PID controller has been tuned using ZN method,DE&HDE technique. However DE&HDE is optimized by ITAE gives better performance than ZN .Between DE & HDE, HDE gives betterperformance than other techniques. |
CONCLUSION |
| PID controller has been tuned using Ziegler-Nichols method, Differential Evolution and Hybrid Differential Evolution for a composite control system. The various results presented above better performances of PID controller tuned with DE, HDE than PID controller tuned with Ziegler-Nichols method. The step responses for the system reflect effectiveness of the HDE based PID controller in terms of time domain specifications. The results show that the proposed controller can perform an efficient search for the optimal PID controller parameters. |
References |
|