Two Pattern Test Cubes for Transition Path
Delay Faults Test for ISCAS-85 C432

T.Vishnu Murty; G.Seetha Mahalakshmi

Two Pattern Test Cubes for Transition Path Delay Faults Test for ISCAS-85 C432

T.Vishnu Murty¹, G.Seetha Mahalakshmi²

M.Tech, Asst. Professor, Dept of Electronics & Communication Engineering, Pragati Engineering College, Surampalem, AP, India
M.Tech Student, Dept of Electronics & Communication Engineering, Pragati Engineering College, Surampalem, AP, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Considering full-scan circuits, incompletely-specified tests, or test cubes, are used for test data compression. When considering path delay faults, certain specified input values in a test cube are needed only for determining the lengths of the paths associated with detected faults. Path delay faults, and therefore, small delay defects, would still be detected if such values are unspecified. The goal of this paper is to explore the possibility of increasing the number of unspecified input values in a test set for path delay faults by un specifying such values in order to make the test set more amenable to test data compression. Experimental results indicate that significant numbers of such values exist. The proposed procedure unspecified them gradually to obtain a series of test sets with increasing numbers of unspecified values and decreasing path lengths. Experimental results also indicate that filling the unspecified values randomly (as with some test data compression methods) recovers some or all of the path lengths associated with detected path delay faults. The procedure uses a matching of the sets of detected faults for the comparison of path lengths.

INTRODUCTION

Test Data compression methods for full-scan circuits use incompletely-specified tests, or test cubes, to accommodate the constraints of test data decompression logic on the tests applicable to the circuit [1]–[4]. An incompletely-specified test is obtained if test generation for a target fault stops as soon as the fault is detected. However, even in this case, due to the order by which inputs are considered during test generation, a test may contain specified values that are not necessary for the detection of the fault. Due to this possibility, dynamic test compaction procedures include processes that increase the numbers of unspecified values in a test without losing the detection of target faults [5], [6]. Dynamic test compaction procedures use the unspecified values for detecting additional faults by the same test. However, the specification of additional values can be done under the constraints of a test data compression method. The procedures described in [7] and [8] start from a completely specified test set and unspecified as many input values as possible without reducing the number of detected target faults. The unspecified values can then be used for test data compression.

In the procedures described in [5]–[8], the decision to unspecified an input value in a test made based on its effect on the fault coverage. If the fault coverage is reduced, the input retains its specified value. Otherwise, it is unspecified. This approach, where un specifying input values is guided by the fault coverage, is applicable to any fault model (stuck-at faults are considered in [5]–[8]).

When considering path delay faults for the detection of small delay defects, in addition to the fault coverage, another parameter of a test set is related to the lengths of the paths associated with detected path delay faults. In this case, certain specified input values may be needed only for determining the lengths of the paths associated with detected faults. If such input values are unspecified, one or more path delay faults would still be detected for every originally detected fault. Therefore, small delay defects would continue to be detected. However, the detected faults would be associated with shorter paths. The goal of this paper is to explore the possibility of un specifying input values that affect the lengths of the paths associated with detected path delay faults, thus making a test set for path delay faults more amenable to test data compression.

The terminology used in this paper with respect to path delay faults is the following. A small delay defect has an extra delay that is smaller than the clock period. Path delay faults model the case where the accumulation of small delay defects along a path causes the delay of the path to exceed the clock period. A full path starts from an input and ends at an output of the combinational logic of the circuit. A sub path starts from an internal line or an input, and ends at an internal line or an output. A path can be a full path or a sub path. The importance of sub paths to the discussion of path delay faults results from the fact that the percentage of detectable path delay faults can be low [9]–[13]. To allow small delay defects to be detected even when path delay faults are not detected, path delay faults that are associated with full paths as well as path delay faults that are associated with sub paths are considered in [14]–[16].

To define the conditions under which a path delay fault associated with a sub path is considered to be detected, the transition path delay fault model is used in [16]. A test for a transition path delay fault requires the detection of a transition fault on every line along the path associated with the fault. Tests for transition path delay faults are a special type of strong non-robust tests for path delay faults. A strong non-robust test sensitizes the path by assigning noncontrolling values to off-path inputs during the second pattern of the test. In addition the test creates a 0 1 or 1 0 a transition on every line of the path corresponding to the transition at the source of the path. To detect a transition path delay fault the test is also required to detect each corresponding transition fault along the path.

This paper considers transition path delay faults associated with full paths and sub paths when determining values that can be unspecified under a two-pattern (broadside) test set for a full-scan circuit. The ability to define the detection conditions of a transition path delay fault based on a set of transition faults that need to be detected facilitates the proposed procedure. Starting from a completely-specified test set, denoted by the procedure focuses on scan-in values that can be unspecified. The procedure consists of two parts, as follows.

The first procedure described in this paper ensures that the transition path delay faults that are detected by will continue to be detected after scan-in values are unspecified under. Let P denote the set of transition path delay faults detected by .This procedure does not allow the detection of any fault from P to be lost when is unspecified. This is similar to requiring that the fault coverage of with respect to transition path delay faults would not decrease. It provides a baseline where as many values as possible are unspecified without reducing the fault coverage. This baseline represents the case where the test generation procedure produces incompletely-specified tests to detect a set of target path delay faults. The main contribution of this paper is in allowing additional values to be unspecified in case the test set cannot be compressed by a selected test data compression method, as discussed next.

To allow additional scan-in values in to be unspecified, the second procedure described in this paper allows the lengths of the paths associated with the transition path delay faults in P to be reduced as T is unspecified. For a fault pj that is associated with a path of length Lj, it is possible to consider sub paths of lengths 1<=l<=Lj. The proposed procedure allows path lengths to be reduced to one. It thus allows the detection of a transition path delay fault Pj to be replaced by the detection of each transition fault included in Pj individually. By unspecifying scan-in values gradually, the procedure ensures that the path lengths in P are reduced gradually.

Test data decompression logic applies completely-specified tests, where the unspecified values of a test cube may be filled randomly or based on other, specified values. Randomly filling the unspecified values of a test set produced by the proposed procedure imitates this.

Due to variations in path lengths associated with detected path delay faults that occur when unspecified values are filled randomly, the paper defines a matching between the transition path delay faults detected by the completely-specified test set T to which the proposed procedure is applied, and the test sets produced by the proposed procedure. The matching provides a more accurate assessment of the effects of unspecified values, and of randomly filling these values, on the path lengths associated with detected faults.

Experimental results indicate that randomly filling the unspecified values of a test set obtained by the proposed procedure increases the path lengths associated with detected faults. For the first few test sets in the series produced by the proposed procedure from a test set T, the path lengths are equal or close to those of T.

The discussion in this paper is independent of any particular test data compression method, and targets only the number of unspecified values in the test set. Additional unspecified values are assumed to improve the ability to compress a test set. It is also possible to use the constraints of a particular test data compression method for guiding the proposed procedure to un specified certain input values.

TRANSITION PATH DELAY FAULTS

Path delay faults model small delay defects whose accumulation along a path cause the path to fail. The transition path delay fault model was defined in order to capture the situation where the accumulation of small extra delays is sufficient for causing faulty behavior after a transition is propagated through a sub path. As a result, the model captures both small and large delay defects. This is accomplished as follows.

Similar to a path delay fault, a transition path delay fault is associated with a path and a transition on its first line. When the transition is propagated along the path, it defines corresponding transitions for all the lines of the path. Based on these transitions it is possible to define transition faults along the path. A transition path delay fault is detected when all the single transition faults along the path are detected by the same test.

For the discussion in this paper, a transition path delay fault is denoted by pj=fj,0-fj,1-….fj,L-1,where fj,0,fj1,…fj,L-1 are the transition faults that need to be detected in order to detect pj. The relationship between the faults is the following.

Let fj,l be vj,l v’j,l transition fault on line gj,l. Then gj,o-gj,1…gjL-1 forms a path .In addition vj,l =vj0, if the number of inverters between gj,0 and gj,l is even, and vj,l=v’j,0 if the number of inverters between gj.l and gj,0 is odd. If pj is associated with a full path, a test for pj is a strong non-robust test for the path delay fault associated with gj,0- gj,1-….gj,L-1 and the vj,0 v’j,o transition on gj,0. If gj,0 or gj,Lj-1 is an internal line, the requirement to detect a transition fault on gj,0 guarantees that a test for pj will cause a transition to occur on gj,0 even if it is an internal line. The transition is propagated to gj, Lj-1 under the strong non-robust propagation conditions. The requirement to detect a transition fault on gj, Lj-1 guarantees that a test will propagate fault effects from gj,Lj-1 to an output gj,Lj-1 if is an internal line.

The ease of dealing with sub paths under the transition path delay fault model, and the uniformity in dealing with full paths and sub paths, is one of the reasons for using the transition path delay fault model in this work. The disadvantage of using this model is that fault simulation requires simulation of transition faults under every test, as discussed below. With an appropriate definition for the detection conditions of faults associated with sub paths, the procedures developed in this paper can be applied to other path delay fault models, including ones for which fault simulation requires only logic simulation.

Given a two-pattern test ti, to find the transition path delay faults detected by ti, the procedure from [16] first simulates all the transition faults under ti. Next, the procedure marks all the lines with detected transition faults. It then identifies a set of lines were detected transition path delay faults begin. The set is denoted by B.A line b ÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ B is associated with a detected transition fault. In addition it satisfies one of the following conditions, which ensure that a detected transition path delay fault starting at cannot be extended towards the inputs.

1) b is an input.

2) If b is a gate output, none of the gate inputs is marked as having a detected transition fault.

3) If b is a fan-out branch, the fan-out stem of is not marked as having a detected transition fault.

COMBINATIONAL BENCHMARK CIRCUIT C432

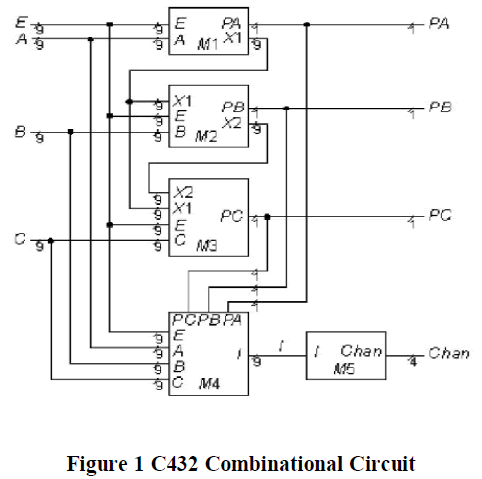
In this proposed method we test 36-bit input ISCAS-85 C432 27-channel interrupt controller. In this method we are test any IC are bench mark circuits. This paper shows that on-chip generation of functional broadside tests can be done using a simple and fixed hardware structure, with a small number of parameters that need to be tailored to a given circuit, and can achieve high transition fault coverage for testable circuits. With the proposed on-chip test generation method, the circuit is used for generating reachable states during test application. This alleviates the need to compute reachable states offline.

SCANING CIRCUITS

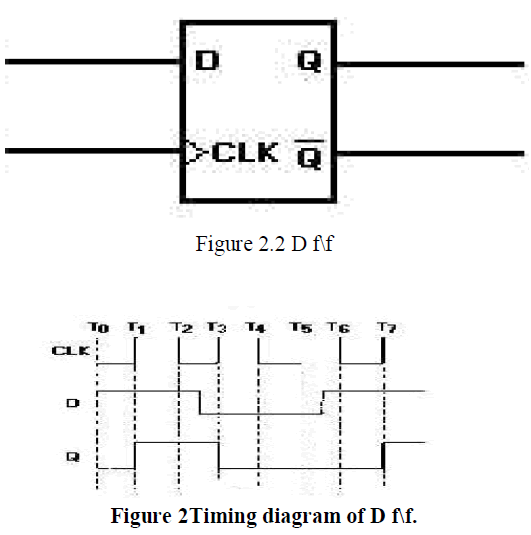
D f\fÃÂ¢Ãâ¬ÃÅ¸s

The D flip-flop is the most common flip-flop in use today. It is better known as data or delay flip-flop (as its output Q looks like a delay of input D).The Q output takes on the state of the D input at the moment of a positive edge at the clock pin (or negative edge if the clock input is active low). It is called the D flip-flop for this reason, since the output takes the value of the D input or data input, and delays it by one clock cycle. The D flip-flop can be interpreted as a primitive memory cell, zero-order hold, delay line. Whenever the clock pulses, the value of Qnext is D and Qprev otherwise.

Stuck at „0ÃÂ¢Ãâ¬ÃÅ¸ Fault

A stuck-at fault is a particular fault model used by fault simulators and automatic test pattern generation (ATPG) tools to mimic a manufacturing defect within an integrated circuit. Individual signals and pins are assumed to be stuck at Logical '1', '0' and 'X'. Likewise the output could be tied to a logical 0 to model the behavior of a defective circuit that cannot switch its output not all faults can be analyzed using the stuck-at fault model. Compensation for static hazards, namely branching signals, can render a circuit untreatable using this model. Also, redundant circuits cannot be tested using this model, since by design there is no change in any output as a result of a single fault. In this model, one of the signal lines in a circuit is assumed to be stuck at a fixed logic value, regardless of what inputs are supplied to the circuit. Hence, if a circuit has n signal lines, there are potentially 2n stuck-at faults defined on the circuit, of which some can be viewed as being equivalent to others. The stuck-at fault model is a logical fault model because no delay information is associated with the fault definition. It is also called a permanent fault model because the faulty effect is assumed to be permanent, (e.g. temperature, power supply voltage) or on the data values (high or low voltage states) on surrounding signal lines. A pattern set with 100% stuck-at fault coverage consists of tests to detect every possible stuck-at fault in a circuit. 100% stuck-at fault coverage does not necessarily guarantee high quality, since faults of many other kinds such as bridging faults, opens faults, and transition (delay) faults often occur.

Fault models are needed to analyze the result of the test n Logical Fault : Representation of the effect of the physical faults on the operation of the system Only the logic function is usually considered (not timing) Logical faults allow a mathematical treatment of testing and diagnosis Assumptions are on side readd to make the analysis feasible. When simulating stuck-at faults, a faulty location can fail in one of two ways. A "stuck at- one" causes the location to simulate as a logic one, or high, value for the entire test. Similarly,” stuck-at-zero” causes the location to simulate as a logic zero, or low, value for the entire test Input pins are trickier. To be sure you have detected a stuck-at-one or stuckat- zero input pin, an output pin must change state as a result of the input being toggled

Statistics: 36 inputs; 7 outputs; 160 gates; bus translations

Function: c432 is a 27-channel interrupt controller. The input channels are grouped into three 9-bit buses (we call them A, B and C), where the bit position within each bus determines the interrupt request priority. A forth 9-bit input bus (called E) enables and disables interrupt requests within the respective bit positions. The figure above concisely represents the circuit. The figure above contains the modules labeled M1, M2, M3, M4, and M5, which contain the underlying logic.

The interrupt controller has three interrupt request buses A, B and C, each having nine bits or channels, and one channel-enable bus E. The following priority rules apply: A[i] > B[j] > C[k], for any i, j, k; i.e., bus A has the highest priority and bus C the lowest. Within each bus, a channel with a higher index has priority over one with a lower index; for example, A[i] > A[j], if i > j. If E[i] = 0, then the A[i], B[i], and C[i] inputs are disregarded.

The seven outputs PA, PB, PC and Chan[3:0] specify which channels have acknowledged interrupt requests. Only the channel of highest priority in the requesting bus of highest priority is acknowledged. One exception is that if two or more interrupts produce requests on the channel that is acknowledged, each bus is acknowledged.

For example, if A[4], A[2], B[6] and C[4] have requests pending, A[4] and C[4] are acknowledged. Module M5 is a 9- line-to-4-line priority encoder. The output line numbered 421 actually produces the inverted Chan[3] response of that shown in the truth table. We have taken the liberty of adding an inverter to output 421 to form Chan[3] for this table (but not in the models).

RESULTS AND ANALYSIS

CONCLUSION

This paper described two procedures for un specifying a two pattern test set for transition path delay faults in full-scan circuits. These procedures un specify scan-in values. This procedure ensures that the same transition path delay faults will be detected by the test set after it is unspecified. To allow additional scan-in values to be unspecified, and thus make the test set more amenable to test data a combinational bench mark circuit is used for test data compression, Results are verified.

References

K. Lee, J. Chen, and C. Huang, “Using a single input to support multiple scan chains,” in Proc. Int. Conf. Comput.-Aided Design, 1998, pp. 74– 78.
C. Barnhart, V. Brunkhorst, F. Distler, O. Farnsworth, B. Keller, and B. Koenemann, “OPMISR: The foundation for compressed ATPG vectors,” in Proc. Int. Test Conf., 2001, pp. 748–757.
B. Koenemann, C. Barnhart, B. Keller, T. Snethen, O. Farnsworth, and D.Wheater, “A smartBIST variant guaranteed encoding,” in Proc. Asian Test Symp., 2001, pp. 325–330.
J. Rajski, J. Tyszer, M. Kassab, N. Mukherjee, R. Thompson, K.-H. Tsai, A. Hertwig, N. Tamarapalli, G. Mrugalski, G. Eide, and J. Qian, “Embedded deterministic test for low costmanufacturing test,” in Proc. Int. Test Conf., 2002, pp. 301–310.
P. Goel and B. C. Rosales, “Test generation and dynamic compaction of tests,” in Proc. Test Conf., 1979, pp. 189–192.
I. Pomeranz, L. N. Reddy, and S. M. Reddy, “COMPACTEST: A method to generate compact test sets for combinational circuits,” IEEE Trans. Comput.-Aided Design, vol. 12, no. 7, pp. 1040–1049, Jul. 1993.
S. Kajihara and K. Miyase, “On identifying don’t care inputs of test patterns for combinational circuits,” in Proc. Int. Conf. Comput.-Aided Design, 2001, pp. 364–369.
A. El-Maleh and A. Al-Suwaiyan, “An efficient test relaxation technique for combinational & full-scan sequential circuits,” in Proc. VLSI Test Symp., 2002, pp. 53–59.
K. Fuchs, F. Fink, and M. H. Schulz, “DYNAMITE: An efficient automatic test pattern generation for path delay faults,” IEEE Trans. Computer- Aided Design Integr. Circuits Syst., vol. 10, no. 10, pp. 1323–1335, Oct. 1991.
U. Sparmann, D. Luxenburger, K.-T. Cheng, and S. M. Reddy, “Fast identification of robust dependent path delay faults,” in Proc. Design Autom. Conf., 1995, pp. 119–125.
S. Kajihara, K. Kinoshita, I. Pomeranz, and S. M. Reddy, “A method for identifying robust dependent and functionally unsensitizable paths,” in Proc. VLSI Design Conf., 1997, pp. 82–87.
K. Heragu, J. H. Patel, and V. D. Agrawal, “Fast identification of untestable delay faults using implications,” in Proc. Int. Conf. Comput.-Aided Design, 1997, pp. 642–647.
S. Padmanaban and S. Tragoudas, “A critical path selection method for delay testing,” in Proc. Int. Test Conf., 2004, pp. 232–241.
K. Heragu, J. H. Patel, and V. D. Agrawal, “Segment delay faults: A new fault model,” in Proc. VLSI Test Symp., 1996, pp. 32–39.
M. Sharma and J. H. Patel, “Testing of critical paths for delay faults,” in Proc. Int. Test Conf., 2001, pp. 634–641.
I. Pomeranz and S. M. Reddy, “Path selection for transition path delay faults,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 18, no. 3, pp. 401–409, Mar. 2010.
I. Pomeranz and S.M. Reddy, “Input necessary assignments for testing of path delay faults in standard-scan circuits,” IEEE Trans. Very Large