International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
MenuISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
M.Thenmozhi, Ms.K.Subhashini
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
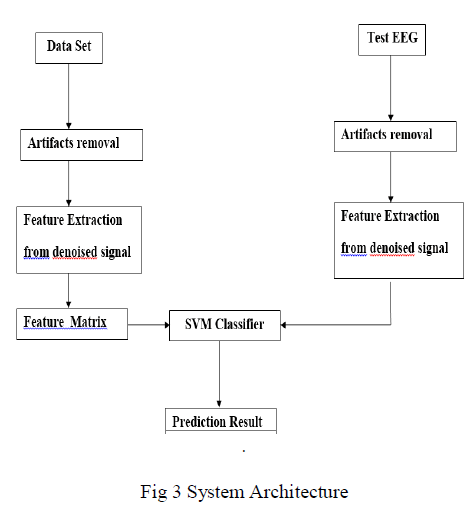
Introduced a new model using DWT and ANC techniques to remove the OAs in contaminated EEG signals. The model is based on discrete wavelet transformation (DWT) and adaptive noise cancellation (ANC). A particularly novel feature of the new model is the use of DWTs to construct an OA reference signal, using the three lowest frequency wavelet coefficients of the EEGs. The results show that the new model demonstrates an improved performance with respect to the recovery of true EEG signals and also has a better tracking performance. The model is also applied and evaluated against data recorded within the EUFP 7 Project—Online Predictive Tools for Intervention in Mental Illness (OPTIMI). The results show that the proposed model is effective in removing OAs and meets the requirements of portable systems used for patient monitoring as typified by the OPTIMI project.After that, artifacts removal signals are received to identify the brain condition and then extract the feature.Features like mean, median ,and wavelet based features are extracted from the signal.The extracted features are classified using SVM classifier. System matches the signals with the true label to decide the condition is occurred in brain
Keywords |
| adaptive noise cancellation; discrete wavelet transformation; electroencephalogram; ocular artifacts; support vector machine |
INTRODUCTION |
| Nervous disorder is exponentially growing challenge in Tele-care and Tele-health projects. Main example is that EEG, the EEG based home care system in Online Predictive Tools for Intervention in Mental Illness (OPTIMI) which is used to monitor the level of each mental disorders and gather the patients information during treatment using EEG signal.EEG is a recording of the electrical activity of the brain from the scalp. The recorded waveforms reflect the cortical electrical activity. |
| EEG signals are measured from conductors positioned on the scalp. The amplitude scalp ranges from 20 to 200μV. |
| EEG frequency ranges from 0.1 to 100Hz and its amplitude is 2 to 200μV. EEG consists of five bands; they are delta, theta, alpha and beta. During EEG acquisition, contaminated from eye movements and blinks also produce serious distortion in the recorded data. These environmental factors produce large electric potential around the eyes called ocular artifacts (OAs). Most often used method to remove the ocular artifacts is either time domain [1] or frequency domain [2] techniques. Later, principal component analysis [3], [4] is used to remove the artifacts but it cannot remove the artifacts completely from EEG because the waveforms of the ocular artifacts are smaller in amplitude when compared to the ongoing EEG signal. |
| In the previous research, independent component analysis [5], [6] is used to remove the ocular artifacts but in this analysis the ICA needs reference signal that requires unexciting classification of components [7], [8]. This techniques is mainly based on wavelet threshold and independent component analysis (ICA) are developed for use in high dimensional neural data. The wavelet techniques uses a discrete wavelet transform with a haar basis function to localize artifacts in time and frequency before removing them with thresholding. In this the wavelet decomposition level is automatically selected based on the smoothness of artifactual wavelet approximation coefficients [10]. The independent component analysis method separates the signal into independent components, detects the artifactual components by measuring the offset between the mead and median of each component, and then removing the correct number of components based on the offset and the power of the reconstructed signal. |
| A quantitative method for evaluating these techniques is also presented. Through this evaluation, the adaptation of wavelet thresholding to produce admirable reduction of ocular artifacts when compared to the other techniques. In this paper a new model is introduced to remove the artifacts using adaptive noise cancellation and discrete wavelet transform and the most important thing is, we have to construct the reference signal. In this the discrete wavelet transforms to the contaminated signal to derive the reference signal and then it is used in the next stage of ANC. The main advantage of ANC is that it can follows the changes and automatically adjust its parameter ANC is used to remove the noise from the reference signal and often used to remove the power line interference in the EEG signal. After that artifacts removal signals are received to identify the brain condition and then extract the features. Features like mean, median ,and wavelet based features are extracted from the signal. The extracted features are classified using SVM classifier. Given signals are tabulated to classify each signals. True label is set for normal and abnormal signals . System matches the signals with the true label to decide the condition is occurred in brain. |
II. DESIGN |
| The recorded EEG signals are contaminated by OAs, this contamination is considered to be an additive noise within the EEG signal. |
 |
A. Discrete Wavalet Transform |
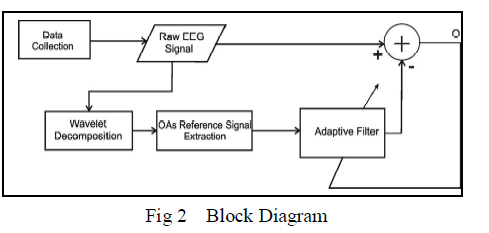
| In this model, the wavelet decomposition is used to construct a reference signal and then produce the denoised signal by the use of adaptive noise cancellation. The de-noised signal is helpful for producing more accurate measurements of latency and time. |
B. Adaptive Noise Cancellation |
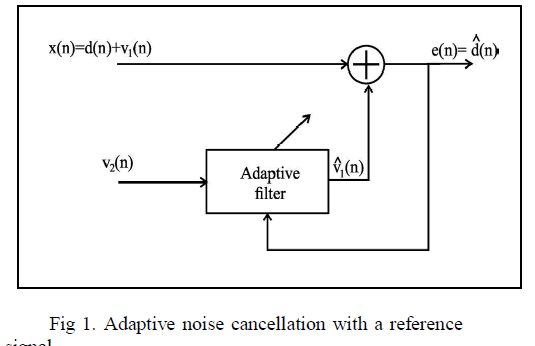
| The noise cancellation in which a process d(n) is to be estimated from a noise corrupted observation |
 |
| without any information about d(n) or v1(n) it is impossible to separate the signal from the noise. Fig 1 However, given a reference signal v2(n),that is correlated with v1(n) then this reference signal may be used to estimate the noise v1(n) and this estimate may then be subtracted from x(n) to form an estimate of d(n) |
 |
If the reference signal v2(n) is uncorrelated with d(n), then minimizing the mean square error  is equivalent to minimizing  .In this model, the adaptive noise cancellation is mainly used to remove the noise from the reference signal. An alternative method of estimating signals corrupted by additive noise interference is to use an ANC adaptive filter [9], [10]. In an ANC filter, the interference source is used as a reference when adjusting coefficients automatically to achieve optimal filtering. |
C. LMS and RLS |
| The core of adaptive filter is the adaptive algorithm From that the most commonly used algorithm is least mean square and recursive least square. In the adaptive system, it is based on LMS algorithm. It has good performance when the environmental noise is a stationary random signal. |
 |
| If the noise is unstable then the LMS has difficult in tracking the noise adaptively as the statistical properties changes. |
| So, in this model it use RLS algorithm in the adaptive filter because when compared to LMS, the RLS has good performance in a non-stationary environment and is able to track slowly varying parameters. ANC is mainly based on RLS algorithm and it is used to remove the OAs from the EEG signal. The filter adjusts its coefficients in accordance with the weighted square error and minimum standard deviation to get the optimal filter coefficients. |
 |
A. Module Description |
| A. Module Description |
| 1. Wavelet decomposition is used to decompose signals into multi-scale representations. It is a commonly used tool for analyzing non-stationary signals. The wavelets used in DWT are effective in constructing both time- and frequency-domain information from time-varying and non-stabile EEG signals. Unlike the Fourier transform, the wavelet transform can use a variety of different basis functions with differing properties. There has been much research on the use of DWT to remove the artifacts in EEG signals. |
| 2. According to the minimum risk value, we have to select the soft threshold and apply them to the three lowest level coefficients to get the new coefficient for those levels. The soft threshold is mainly used to make the wavelet coefficients contract to zero according to a fixed vector. The threshold value is given by |
 |
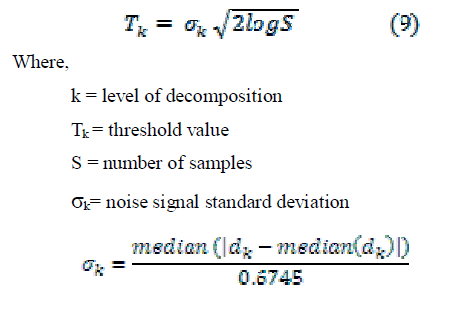| 3. Here, we apply wavelet reconstruction to the new wavelet coefficients for constructing the reference signal. |
 |
 |
| 4. ANC based on the RLS algorithm is used to remove the OAs from the EEG signal |
| 5. Artifacts removal signals are received to identify the brain condition . Features like mean, median ,and wavelet based features are extracted from the signal.The extracted features are classified using SVM classifier |
| 6. Given signals are tabulated to classify each signals. True label is set for normal and abnormal signals . System matches the signals with the true label to decide the condition is occurred in brain |
IV.RESULT AND DISCUSSION |
| Thus, after specifying these models the simulated noisy EEG signal is obtained. Each simulated EEG waveform contains 5120 samples and its sampling frequency is 256 Hz.. |
 |
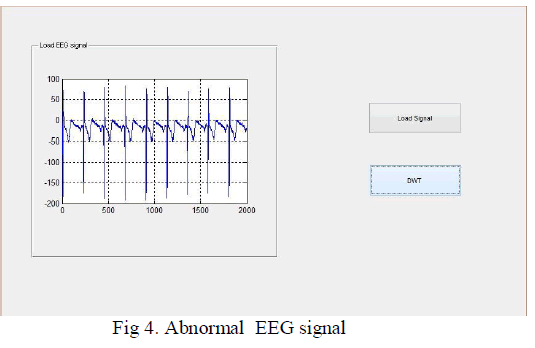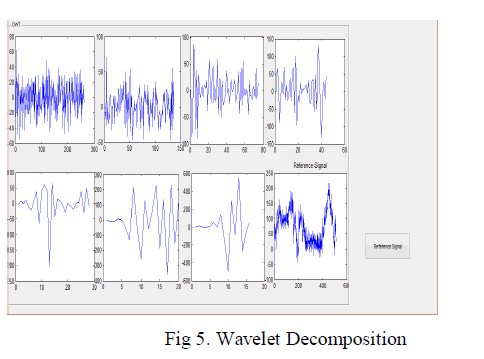
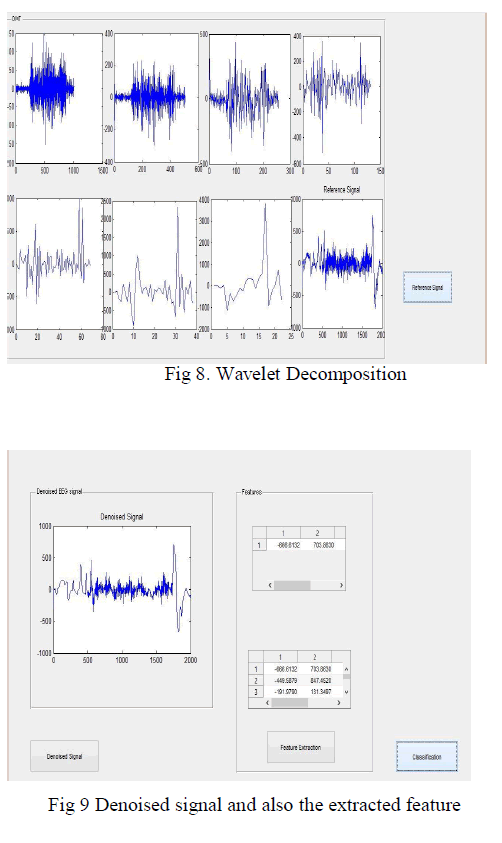
| The level of the wavelet decomposition is too small, it is difficult to remove the noise effectively; however, if the decomposition level is too high, the signal to-noise ratio is poor. We, therefore, selected seven layers of decomposition as a compromise. Fig 5. Shows the seven levels of wavelet decomposition for constructing the reference signal. |
 |
| The accuracy of each model was measured by comparing e(n) with the true EEG x(n) in the time and frequency domains. Here ,we calculate PSNR value by the use of MSE.MSE is given by, |
 |
 |
 |
 |
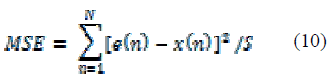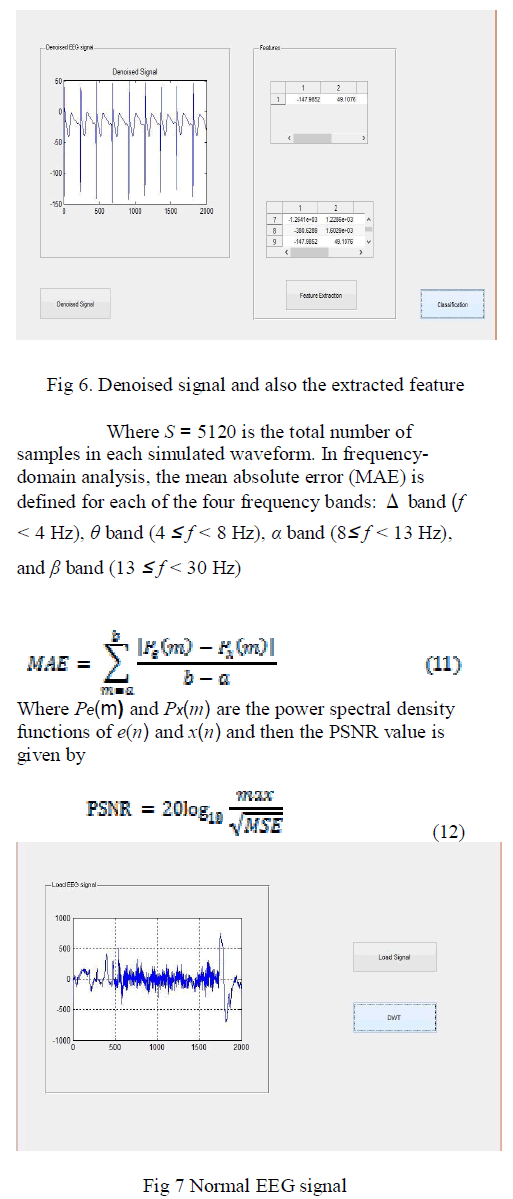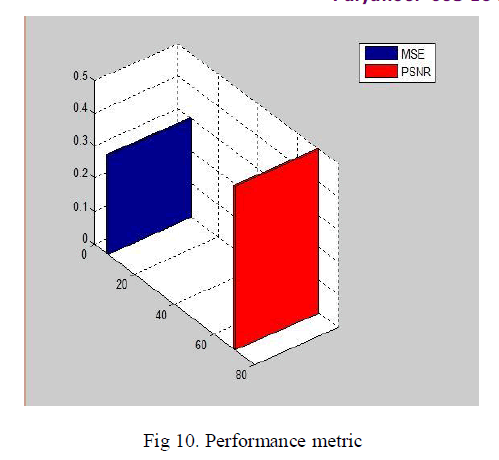| In the previous model, the PSNR vale is 51.19 db but in this model the PSNR value is 70.4618 db |
| Thus, the new model using DWT and ANC techniques to remove ocular artifacts in contaminated EEG signals. The above work demonstrates the effectiveness of the new model by using the model to process simulated and standard EEG data. The proposed method eliminates Ocular artifacts in the low frequency band even when their frequency is overlapping with that of the EEG signal. Using simulated data, it has been established that the superior performance of the proposed model does adversely affect the performance of the model with respect to the application of ICA. Therefore conclude that with respect to other concepts in this area the proposed model is able to provide better attenuation levels for common types of OA’s present in EEG signals |
References |
|