Using Painleve Test on the Kinetic System
for Yang-Mills Theory

Ahmed Kamil

Using Painleve Test on the Kinetic System for Yang-Mills Theory

Ahmed Kamil
Department of Theoretical Physics, Faculty of Physics and Mathematics, Moscow, 117198 ,Russian

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

We study the Yang-mills theory as a kintic system, and used C. Becchi, A. Rouet and R. Stora; transformation to Renormalization of gauge theories, test the random of the system by use the painleve test

Keywords

Yang-Mills theory, Painleve Test.

I. INTRODUCTION

Yang-Mills theory is a non-Abelian gauge theory, and we used a lot in QCD calculation, the yang- mills theory is the most important in physics in the last fifty years. Yang-Mills theory was first discovered in the 1950, at this time, quantum electrodynamics was known to describe electromagnetism [1]. Yang–Mills theory seeks to describe the behavior of elementary particles. In 1954, Yang and Mills published a paper on the isotopic SU(2) invariance of the proton-neutron system [2]. Yang-Mills theory plays a central role in explaining fundamental interactions ,because both the strong and weak interactions are described by Yang-Mills theories [3].Yang-Mills theory allow one to describe both the Maxwell electromagnetic interactions and the Fermi weak interactions and to obtain the known value of the (Z0) boson (weak boson) mass. Yang-Mills gauge theory with gauge group SU(3)×SU(2)×U(1). Here the first factor is the gauge group of QCD while (SU(2)×U(1)) gauge field is that transmitting what is called the electroweak force [4].

II. THE MODEL

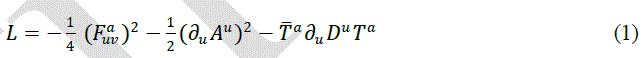III. CONCLUSION

Using the lagrangian of Yang-Mills theory [5]. introduceing C. Becchi , A. Rouet , R. Stora and I.V. Tyutin for transformation to Renormalization of gauge theories [6]. test the random of the system by use the painleve test [7]. Finally We found that yang-mills theory is non-integrable according to Painleve test.

References

Davies, C. 2002, Lattice QCD, London: Institute of Physics.
C. N. Yang and R. Mills, Phys. Rev. 96, 191 (1954).
Addison-Wesley, the role of gauge theory in describing fundamental interactions is described in C.Quigg, Gauge theories of the strong, weak and Electro-magnetic interactions ( New York, 1993).
Andreas Aste, Michael Dütsch, Günter Scharf, Perturbative gauge invariance: electroweak theory II, Annalen Phys.8:389- 404,1999 (arXiv:hep-th/9702053).
S.G. Matinyan, G.K. Savvidy & N.G. Ter-Arutunian Savvidy ; Stochasticity Of Classical Yang-mills Mechanics And Its Elimination By Higgs Mechanism, Published in JETP Lett. 34 (1981) 590-593.
C. Becchi, A. Rouet & R. Stora ; Renormalization of gauge theories, Ann. Phys. 98, 2 (1976) pp. 287–321.
F.Cariello and M.Tabor, painleve expansions for nonintegrable evoulution equations. Physica D, 39:77-94,1989.
L.D. Faddeev, V.N. Popov ; Feynman Diagrams for the Yang-Mills Field., Published in Phys.Lett.B25:29-30, (1967) doi:10.1016/0370- 2693(67) 90067-6. English Version in: 50 years of Yang-Mills Theory by G. ‘t Hooft; World Scientific Books (2005).