Water Displacement and Bulk Density- Relation Methods of Finding Density of Powdered Materials

B. Dan-Asabe; S. A Yaro; D. S Yawas; S. Y Aku

Water Displacement and Bulk Density- Relation Methods of Finding Density of Powdered Materials

B. Dan-Asabe ¹, S. A Yaro ², D. S Yawas³, S. Y Aku⁴

Research Fellow, Shell Chair Office, Department of Mechanical Engineering, Ahmadu Bello University, Zaria
Shell Professor, Shell Chair Office, Department of Mechanical Engineering, Ahmadu Bello University, Zaria
Reader, Department of Mechanical Engineering, Ahmadu Bello University, Zaria
Professor, Department of Mechanical Engineering, Ahmadu Bello University, Zaria

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Determination of true density of particulate substances is very essential particularly during formulation of particulate composite materials. Production of particulate composite materials requires knowledge of the true densities of the individual constituents’ substances as this is essential in material selection especially if composite material of light-weight is so desired. Water displacement method of finding density of insoluble substances is very cumbersome and liable to error hence a bulk density-relation technique was devised to determine true densities of insoluble particulate substances. A case study of Kankara clay using the bulk density-relation (with known densities of calcium carbonate and PVC) was used to determine its true density. Comparison of the methods shows that bulk densityrelation gives a better result with higher degree of accuracy. The results found the density of Kankara clay to be approximately 1.8g/cm3 obtained using the bulk density-relation. Weight density relation was also determined to enable production of composite according to mass mixture proportion

Keywords

Kankara clay; true density; bulk density; volume fraction; weight fraction; water displacement; particulate substance

INTRODUCTION

True density of a substance is defined as the ratio of its compacted mass to its volume devoid of air space. Determination of true density of powdered substances is very important to the pharmaceuticals [1], manufacturing i.e. material recycling [2] and research and development industries. Volume of particulate substance measured using measuring cylinder does not give the true volume since it is inclusive of void spaces filled by air. The pharmaceutical industries use the bulk density in preparation of drugs. Bulk density is defined as oven-dry mass of particulate sample (i.e. a wood chip) divided by bulk volume (in a measuring cylinder) when the chips are packed without compression [3]. The substance should be shaken in a measuring cylinder before reading its volume. Bulk density considers both solids and pore space where as particle density (true density) considers only the mineral solid [4].

Composites provide desired properties that may not be achieved from the individual constituents [5]. Composite materials are classified based on structural design i.e. type of reinforcing element and its disposition in the matrix; material type i.e. type of matrix and reinforcements and their properties; processing technology i.e. production process [6].

Determination of true density of individual constituents in composite material is very essential in material selection especially if composite material of light-weight is so desired. Combination of the constituent to achieve this will mean their true densities must be known. Many natural materials such as Kankara clay, pineapple fibre, coconut fibre, sisal etc (Samuel et al, 2012) find increasing use and acceptance in production of composite materials due to their light weight. Some of these materials are either in fibrous or particulate forms and have known densities while others

are yet to be determined. The unknown (true) density of the natural material in particulate form needs to be known (effective material selection) to give an idea of the resultant weight of the composite.

Production of particulate composite materials requires knowledge of the true densities of the individual constituents’ substances so that after the production of the composite, a comparison will be made to standard composite volume-ratio theory as given below [7];

METHODOLOGY

This is categorized according to the experimental procedure to be carried out using the water displacement method and the bulk density-relation method. A case study of Kankara clay [8] found in Kanakara in Katsina state of northern Nigeria is the particulate substance whose true density is to be determined.

A. Water Displacement

The equipments required are a digital weighing balance, a measuring cylinder, distilled water and the insoluble substance (Kankara clay) whose density is to be determined. A sample of the Kankara clay is weighed in a digital balance and then its volume subsequently measured in a measuring cylinder. The measured volume (bulk volume) is not the actual (true) volume since there’s pore (air space) inclusive in the volume. Measured quantity of distilled water is a then added unto the cylinder and the final volume noted. The is following expression is then used to calculate the density;

Mass of Kankara clay sample, m1

Volume of distilled water, V1

Volume of distilled water and Kankara sample, V2

True density,

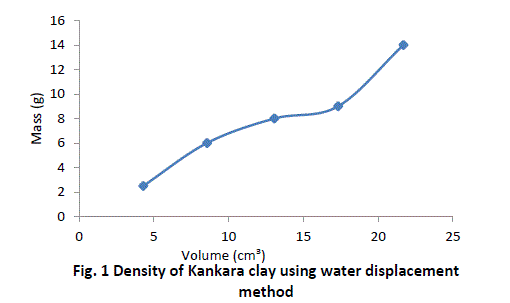
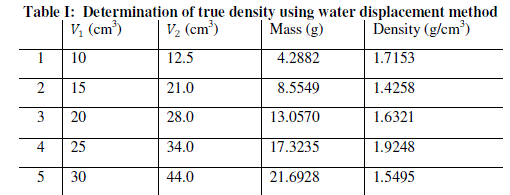
The procedure is repeated for four more samples of Kankara clay at different mass and given in Table 1.

The graphical trend in Fig. 1 shows that the density line is not linear i.e. the density value is not uniform and hence not very reliable. However, a method was devised called the bulk density-relation as discussed below.

B. Bulk density-relation

The bulk density-relation is a procedure I devised and defined as finding the bulk density of a powdered material and subsequently determining its (actual) density in relation it to a known density of another (other) standard powdered material(s). This involves relating the density of one or more standard powdered material with known true density to determine that of the unknown powdered substance i.e. Kankara clay. The equipment required are a digital weighing balance, a measuring cylinder, standard samples and the insoluble substance (Kankara clay) whose density is to be determined In this method, laboratory procured samples of calcium carbonate and PVC are to be used as the standard materials with known true densities and Kankara clay is to be the substance with unknown true density. The bulk densities of the standard material and the Kankara clay are first determined as given below;

Mass of Kankara clay sample, mk

Mass of PVC, mp

Bulk volume of Kankara sample, Vbk

Bulk volume of calcium carbonate sample, Vbc

Bulk volume of PVC sample, Vbp

Bulk densities of the Kankara clay, lime and PVC are calculated below;

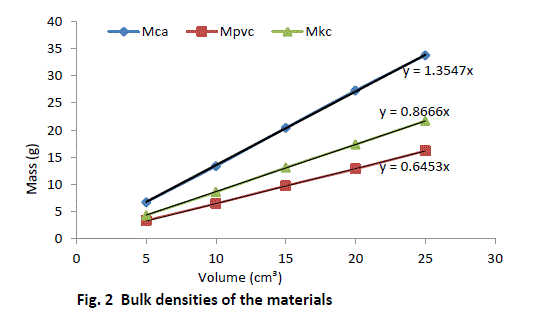
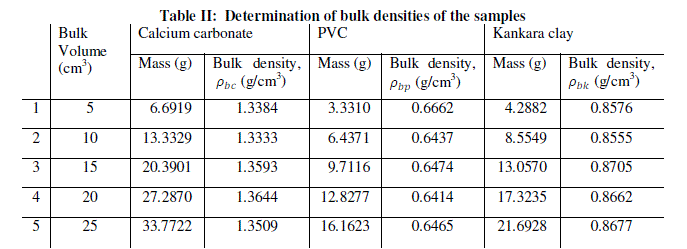
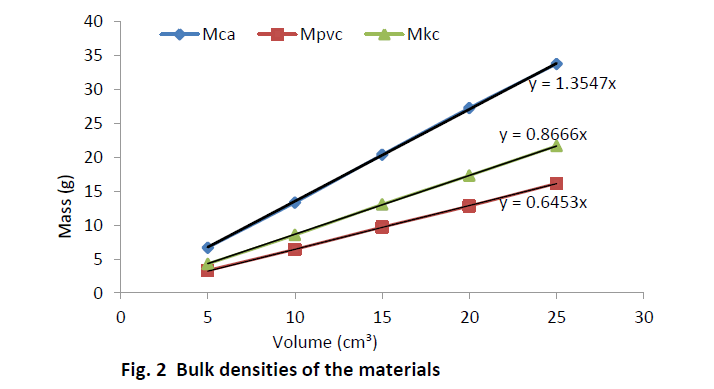
Equal volumes of Kakara clay, lime and PVC measured in a calibrated cylinder are weighed and their respective bulk densities calculated using the above equation (8). The procedure is repeated for four more samples at different volumes and the tabulated as given in Table 2.

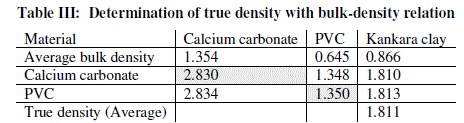
The relation (equation 10) is used to calculate the true density of Kankara clay as calculated in Table 2. Assuming the materials will cover the same true volumes in solid form (say Kankara clay and calcium carbonate with true densities Ρtk and ρtc respectively), we have;

Table 3 relates the bulk densities of the different materials (slopes of Fig. 2) and the standard (known) true densities of calcium carbonate and PVC. The first row depicts the materials whose bulk density and true densities are to be compared with (or related). The second row gives the bulk densities of the materials. The third row indicates that calcium carbonate is used as a standard material with known true density and is used to find those of PVC and Kankara clay. The fourth row indicates that PVC is used as a standard material with known true density and is used to find those of calcium carbonate and Kankara clay. The fifth row gives the average (from the 3rd and 4th row) true density of the unknown Kankara clay as 1.8g/cm3

C. Precautions using the Bulk density-relation

It is necessary to abide by the following precautions:

1. First determining the density of water (distilled) using the measuring cylinder to establish any possible error reading on the cylinder. The density of water at about 25Ãâ¹ÃÅ¡C is 0.995 – 1 g/cm3 [9].

2. Ensuring that material whose density is to be found and the standard material have the same particles size. This is done by sieving with the same sieve size (i.e. 250um sieve).

3. Uniform tapping for compaction settling must be adhered to for all varying sample quantities and the different materials. Typical tapping could be tapping the measuring cylinder (i.e. 100cm3 size) containing the sample with the hand (i.e. about three times with middle finger) in the air and tapping the cylinder on a table or a vibrating device. It must be noted that whichever tapping method used must be adhered for all the samples.

4. Care must be taken to ensure that the density graphical trend is linear. This will mean compaction volume for (varying) sample quantities are uniform.

RESULT AND DISCUSSION

The result shows that determination of true density using water displacement method does not give a stable result. This explains why the slope (Fig. 1) of the curve is not perfectly linear i.e. averaging the density from this does not give reasonable result. Significant effort with many trials can be made to have a fairly linear trend though this is very cumbersome and uneasy to achieve. Result from the bulk density-relation (Fig. 2) shows that the bulk density of the different materials are perfectly linear and passes through the origin (equation of the lines). This shows from the method that density is uniform (for different sample measurement) indicating a reasonable high degree of accuracy. Also, using the bulk density-relation equation with either of each standard specimen (calcium carbonate and PVC) gives the true density of the Kankara clay with high degree of correlation (Table 3).

A check can also be used to determine the accuracy of the result. This is done by checking the density of say PVC (Table 3) using standard true density of calcium carbonate, indicating that the density is very close to that of the standard PVC. Similarly for calcium carbonate it shows that its density is approximately equal to that of its standard one using standard PVC density as reference.

CONCLUSION

Determination of true volume of powdered insoluble substances using water displacement method is very cumbersome and liable to error hence a bulk density-relation technique was devised to determine true densities of insoluble particulate substances. A case study of Kankara clay using the bulk density-relation was used to determine its true density. Comparison of the methods shows that bulk density-relation gives a better result with higher degree of accuracy. The results found the density of Kankara clay to be approximately 1.8g/cm3 obtained using the bulk densityrelation. Weight density relation was also determined for two or constituent materials to enable production of composite according to mass mixture proportion.

References

WHO. Bulk density and tapped density of powders: Final test for addition to the International Pharmacopoeive Document QAS/11.450 FINAL. World Health Organisation, pp 1-6, 2012.
Resource Future. Material bulk densities: Material change for a better enviroment. www.wrap.org.uk/local_authorities, pp. 1-13, 2009.
SCAN-CM Bulk density: Wood chips for pulp production. Scandinavian pulp, paper and board testing committee, 46:92, 1992
Plant & Soil Sciences eLibrary. Soils-Part 2: Physical properties of soil and soil water. Passel.unl.edu/pages/info., accessed 18th September, 2013
Reddy, J. N. Theory and Analysis of Laminated Composite Plates. Kluwer Academic Publishers, Texas, 1999.
Akbarov, S. D. and Guz, A. N. In Mechanics of curved composites (p. 1). Dordrecht: Kluwer Academic Publishers, 2000.
Ashby, M. F. Material Selection in Mechanical Design. Butterworth Hememann, 4th Edition, Oxford, UK, 2011.
Lori, J. A., Lawal, A. O. and Ekanem, E. J. Characterisation and optimisation deferration of Kankara clay. ARPN Journal of Engineering and Applied Sciences, Vol. 2(5), pp. 60- 74, 2007.
Engineering Tool Box (2013). http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html, accessed 14th July, 2013.