ISSN: 2229-371X
ISSN: 2229-371X
Arindam Garai 1*and Tapan Kumar Roy2
|
| Corresponding author: Arindam Garai, E-mail: fuzzy_arindam@yahoo.com |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at Journal of Global Research in Computer Sciences
This paper presents weighted intuitionistic fuzzy Delphi method. In real life usage of Delphi method, information communicated by experts may not be used with full and complete potential. Hence highly accurate and realistic conclusions cannot always be obtained. In intuitionistic fuzzy Delphi method, communication with experts is the same as fuzzy Delphi method, yet an improved and elaborative statistical tool is used to reach in better conclusions. Again, the experts use their individual competency and subjectivity. And competency and ability to predict successfully varies extensively among experts. Thus different importance and hence weights should be assigned to them by the decision maker. Hence more realistic and accurate prediction is obtained.
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Haberler
Key Word |
| Intuitionistic fuzzy Delphi method, Intuitionistic fuzzy decision making technique, Weighted Delphi technique. |
INTRODUCTION |
| The Delphi Method [5] is a well structured communication technique. It was originally developed as a systematic and interactive forecasting method that relies on a panel of experts. It belongs to the subjective-intuitive methods of foresight. Delphi was first developed in the 1940s by the Rand Corporation, Santa Monica, California, in operation research. Different approaches were tried, and to combat the many shortcomings, the Delphi Method was developed by Project RAND during the 1950-1960s (1959) by Olaf Helmer, Norman Dalkey and Nicholas Rescher [14]. |
| The name can be traced back to the Delphic oracle, as Woudenberg reports that the name „DelphiâÃâ¬ÃŸ was intentionally coined by Kaplan, an associate professor of philosophy at the UCLA working for the RAND corporation in a research effort directed at improving the use of expert predictions in policy making. The temple was the locus of knowledge, i.e. the Delphic oracle was probably the largest database of the ancient world [14]. |
| Overall the track record of the Delphi Method is mixed. There have been many cases when the method produced poor results. One may attribute this to poor application of the method and not to the weaknesses of the method itself. It must also be realized that in areas such as science and technology forecasting, the degree of uncertainty is so great that exact and always correct predictions are impossible, so a high degree of error is to be expected! |
| Despite these shortcomings, today the Delphi Method is a widely accepted forecasting tool and has been used successfully for thousands of studies in areas varying from technology forecasting to drug abuse [12]. |
| Several modifications and improvements have appeared in Delphi method [1]. On the other hand, one of the largest shift from traditional classical mathematics happened by the introduction of fuzzy set theory [6]. Fuzzy Delphi method was developed to include and interpret the uncertainty involved in expertsâÃâ¬ÃŸ opinion [2]. |
| Next, fuzzy set theory was further studied and intuitionistic fuzzy set theory was introduced by K. T. Atanassov [3] [11]. And fuzzy Delphi method was further developed. In 2012, the authors studied Delphi technique under intuitionistic fuzzy environment [13]. |
| It is assumed till date that the capability and competency to predict are equal among experts. But this is not true always. It varies! Hence, in this study, the experts have been assigned different importance and hence weights. For simplicity, normalized weights are being used. This helps in forming smarter (!) sheaf of experts that leads to more effective and accurate prediction. |
DEFINITION |
Delphi Method |
| Wechsler (1978) characterizes a „Standard Delphi MethodâÃâ¬ÃŸ in the following way: „It is a survey which is steered by a monitor group, comprises several rounds of a group of experts, who are anonymous among each other and for whose subjective-intuitive prognoses a consensus is aimed at. After each survey round, a standard feedback about the statistical group judgment calculated from median and quartiles of single prognoses is given and if possible, the arguments and counterarguments of the extreme answers are fed back…âÃâ¬ÃŸ [14]. |
| The Delphi Method is based on structural surveys and makes use of the intuitive and available information of the participants, who are mainly experts. Therefore it delivers qualitative as well as quantitative results and has beneath its explorative, predictive even normative elements. There is not the one Delphi methodology but the applications are diverse. There is agreement that Delphi is an expert survey in two or more „roundsâÃâ¬ÃŸ in which in the second and later rounds of the survey the results of the previous round are given as feedback. Therefore, the experts answer from the second round on under the influence of their colleaguesâÃâ¬ÃŸ opinions. Thus, the Delphi Method is a „relatively strongly structured group com-munication process, in which matters, on which naturally unsure and incomplete knowledge is available, are judged upon by expertsâÃâ¬ÃŸ. |
Fuzzy Set |
| A fuzzy subset à of X is defined by its membership function Ã: X [0, 1] that assigns to every x X, a real number à (x) in the closed unit interval [0, 1], where the value of à (x) at x represents the grade of membership of x in à [6]. |
| Nearer the value of Ã(x) is unity, the grade of membership of x in Ã. When the membership function Ã(x) contains only two points 0 and 1, membership function Ã(x) is identical to the characteristic function : X [0, 1] and in that case à is a crisp set. |
Intuitionistic Fuzzy Set |
| An intuitionistic fuzzy set [3] A in X is defined by A = {< x; μA(x), νA(x) > | x X}, where μA: X [0, 1] and νA: X [0, 1] with the condition 0 ≤ (μA(x) + νA(x)) ≤ 1, where μA(x) and νA(x) denote the degree of membership and non membership respectively [7]. |
FUZZY DELPHI METHOD |
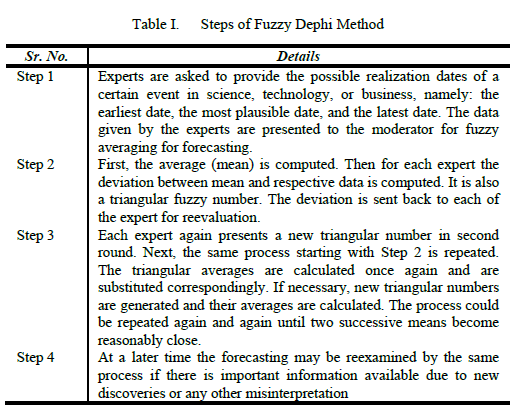
| Fuzzy Delphi Method [5] was first introduced by Kaufman and Gupta in 1988 and it was also proposed by Ishikawa et al. (1993). Noorderhaben (1995) had indicated that applying the Fuzzy Delphi Method to group decision can solve the fuzziness of common understanding of expert opinions. The expert prediction (or interval value) was then used to derive the fuzzy numbers, resulting in the Fuzzy Delphi Method. Hence, Fuzzy Delphi Method is a generalization of the classical method [8]. It consists of the following steps: |
 |
INTUITIONISTIC AND WEIGHTED INTUITIONISTIC FUZZY DELPHI METHOD (WIFDM) |
| Intuitionistic fuzzy Delphi method was introduced in 2012 [13]. The arguments that can be used in favour of using triangular intuitionistic fuzzy numbers (TIFNs) in place of triangular fuzzy numbers (TFNs) are that subjective information that may be transformed into objective values as required in Fuzzy Delphi Method cannot always be obtained. Subjective information is more likely to be like quasi-objective data in case of intuitionistic fuzzy number and hence the use of intuitionistic fuzzy number is more justified. In case of intuitionistic fuzzy Delphi method, communication with experts is the same as fuzzy Delphi method yet a more improved and elaborative statistical tool is used to reach in better conclusions. The experts use their individual competency and subjectivity and are somehow uncertain to air their opinions. Hence, they tend to secure their opinions. Thus, they prefer degree of non-membership over degree of membership and this is the very reason why use of intuitionistic fuzzy concepts is more relevant than fuzzy concepts. Moreover, by using TIFNs, it is easier for an expert to study the realization data which are nested within one another than TFNs. And, the concept of sheaf of intuitionistic fuzzy number is an aggregation process which appears to be very convenient for the objectification of (somehow hazy) subjective opinions. On the other hand, among a group of experts, competency and ability to successfully predict varies to great extent among experts. It is well known that Nouriel Roubini had successfully predicted global recession of 2009 in as early as 2007. Many economists called him Mr. Doom! Yet, it was exactly that! In real life situations, decision maker may assign varied importance to expertsâÃâ¬ÃŸ efficiency (from past experience or level of accuracy or any other pre defined criteria). Importances are calculated in mathematics by assigning respective weights. Weights are assigned to each expert. For simplicity, normalized weights are being used here. If there are n experts, their weights may be assigned as |
 |
 |
CASE STUDY: TIME ESTIMATION FOR TECHNICAL REALIZATION OF AN INNOVATIVE PRODUCT |
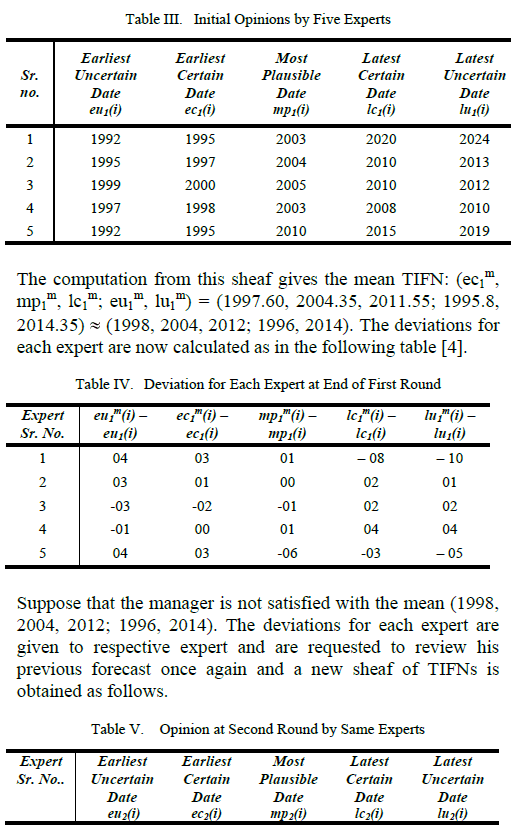
| The data required for the problem of the technological realization of a cognitive information processing computer (as used partially in literature for the sake of simplicity alone). Opinions of five experts only are considered. Here it was requested to a group of five computer experts to give a subjective estimation for the realization of new computing technology in the format of intuitionistic fuzzy number i.e. it will consist of the earliest certain date ec1(i), the earliest uncertain date eu1(i), the most plausible date mp1(i), the latest certain date lc1(i) and the latest uncertain date lu1(i) for each expert Ei. It may be noted that the experts are not ranked equally and hence their opinions carry different weights. Let us take w1 = 0.15, w2 = 0.4, w3 = 0.3, w4 = 0.1, w5 = 0.05 so that |
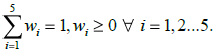 |
| The sheaf formed by expertsâÃâ¬ÃŸ opinions is assumed to be as follows: |
 |
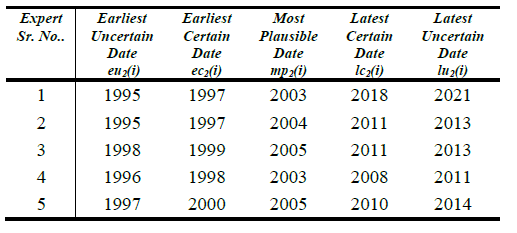 |
| In a similar way, the computation from this sheaf gives the mean TIFN (ec2 m, mp2 m, lc2 m; eu2 m, lu2 m) = (1997.85, 2004.1, 2011.7; 1996.1, 2014.05) (1998, 2004, 2012; 1996, 2014). Now the manager is satisfied because mean TIFN in both cases are same. The process is stopped and the final TIFN is accepted as a combined conclusion of expertsâÃâ¬ÃŸ opinions. This means that the realization of the invention will occur in time interval [1996, 2014] with the inside channel being [1998, 2004] and the most likely year for the realization is 2012. Now, to find the non disjunctive group of experts, the distances between expertsâÃâ¬ÃŸ opinions are calculated. In literature, there is no standard procedure to calculate the distance between TIFNs [9]. Here a technique described in by Arnold Kaufmann, Madan M. Gupta, is further developed [5]. Arnold Kaufmann, Madan M. Gupta used d (Ni, Nj) to be the normalized distance between two TFNs Ni and Nj with |
 |
| It is to be noted that the minimum distance is d (E3, E5) = 0.050 and the maximum distance is d (E1, E3) = d (E1, E4) = d (E1, E5) = 0.275. Now to find pair of experts for whom the distance is less than or equal to 0.1 (denoted by R), the table as below is obtained. |
 |
| For instance, the experts (2, 3), (2, 5) and (3, 5), (4, 5) have given almost same estimation. Opinion of expert 2 is more similar to expert 3 and 5 but not to expert 4. On the other hand, prediction of expert 5 is similar to expert 3 and expert 4. Yet expert 3 does not give similar prediction as expert 4. |
Result and discussion |
| The results clearly indicate that customer is the king. It is ultimately the choice of the Delphi manager i.e. the decision maker. Experts are selected based on some pre defined criterion and are assigned importance. Conclusions depend not only on the choice of experts but also the weights assigned on them. If a good manager or interpreter is found, making futuristic decision will not be a stiff challenge! It is also biggest weakness of the method. If the Delphi manager is unable to select suitable experts or he is not justified enough to assign proper importance (weights), incorrect prediction may be the outcome. To explain and compare, the weakness and strength of each method is discussed in the following table. |
 |
References |
|